Using the DKW inequality to generate a confidence interval for the CDF

27 July 2025

My textbook gave me the exercise of generating 100 observations from a normal \(\mathcal{N}(0, 1)\) distribution then computing the 95% confidence bands for the cdf given these observations then to repeat the experiment for the cauchy distribution.

I did this by using the empirical CDF and the DKW inequality which was introduced earlier in the text.

The empirical CDF is an approximation for the CDF that assigns equal probability weight to each interval between the points in a dataset and the DKW inequality bounds how far the ecdf deviates from the true distribution.

The DKW inequality states that if \(\hat{F}_n\) is an ecdf from a distribution with CDF \(F\) then

\[ P\left(\sup_x \left| F\left(x\right) - \hat{F}\left(x\right) \right| > \epsilon\right) \leq 2e^{-2n\epsilon^2} \]

The statement is simple and applying it is pretty easy but the proof was left out of the textbook, I have no idea how to prove it and the proof looks difficult and a lot of effort [2] so I’m happy to take it as given.

Since I need the probability of the confidence interval containing the CDF to be larger than 95% I need the error probability to be less than 5% and \(2e^{-2n\epsilon^2}\) must be less than 0.05. This gives me freedom to choose any \(\epsilon\) that is larger than \(\sqrt{\frac{-\log\left(\frac{0.05}{2}\right)}{2n}}\).

My R code looks like this

total_experiments <- 1000
sample_size <- 100
alpha <- 0.05
run_experiment <- function (r, p, distribution_name) {
  works <- 0
  for (i in 1:total_experiments) {
    xs <- sort(r(sample_size))
    real <- p(xs)
    ecdf_values <- ecdf(xs)(xs)
    epsilon <- sqrt(-log(alpha / 2) / (2 * sample_size))
    lower <- pmax(ecdf_values - epsilon, 0)
    upper <- pmin(ecdf_values + epsilon, 1)
    if (all(lower <= real) && all(real <= upper)){
      works <- works + 1
    }
  }
  print(
    paste(
      "The normal interval contains our ",
      distribution_name,
      " distribution: "
      100 *  works / total_experiments,
      "% of the time"
    )
  )
}

run_experiment(rnorm, pnorm, "Normal")
run_experiment(rcauchy, pcauchy, "Cauchy")

Here are my graphs from an example experiment

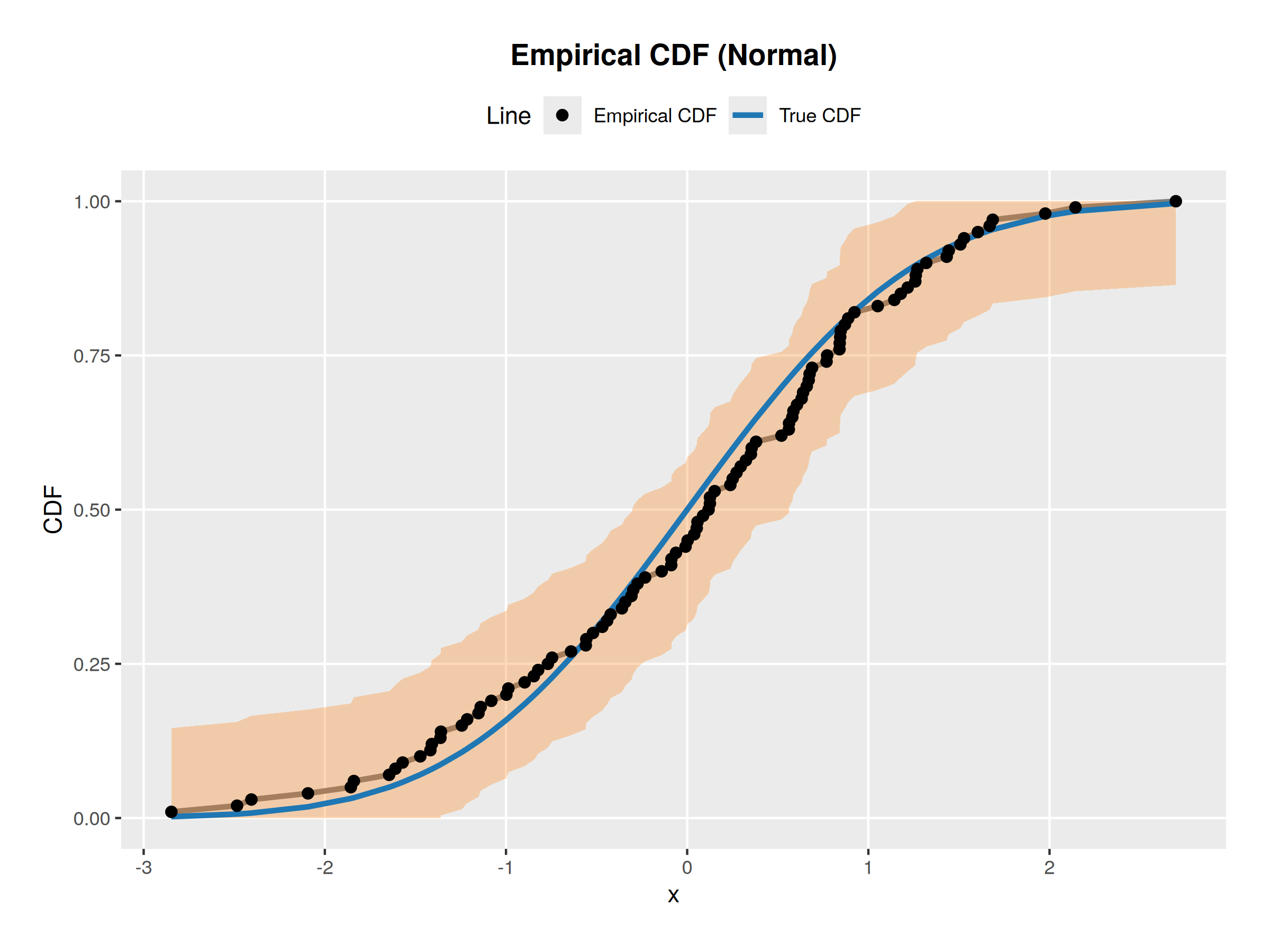
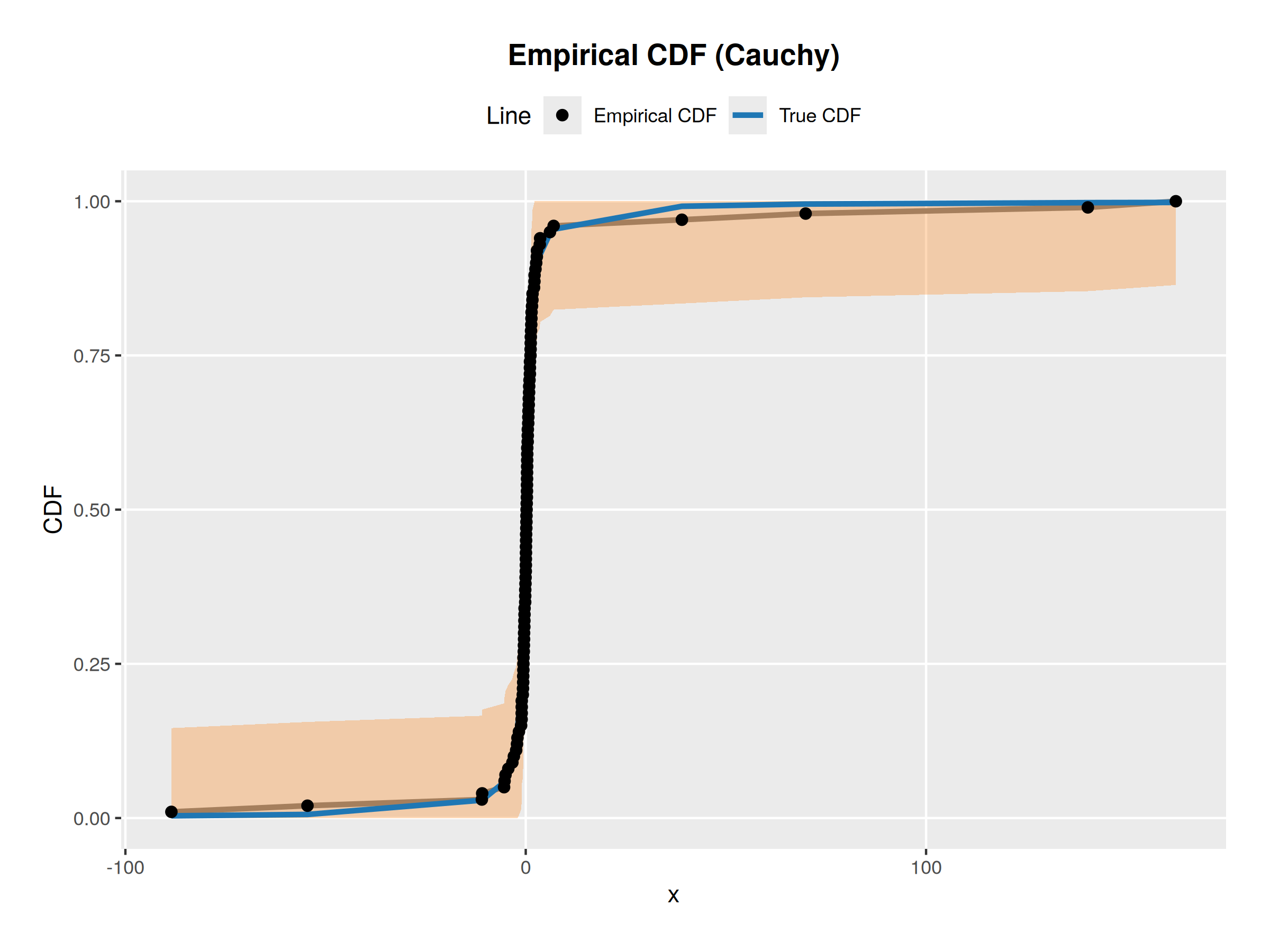
References

[1]: Wasserman, Larry. All of statistics: a concise course in statistical inference. Springer Science & Business Media, 2004.

[2]: Reeve, Henry WJ. “A short proof of the Dvoretzky–Kiefer–Wolfowitz–Massart inequality.” arXiv preprint arXiv:2403.16651 (2024).