Modelling the Limit Order Book as a continuous time Markov Process

Learning about market microstructure

28 December 2024

The Limit Order Book is an order matching method that’s used by most financial exchanges. On an exchange with an order book participants submit buy orders called “bids” and sell orders called “asks” alongside the quantity of the asset that they would like to buy or sell.

As a diagram it looks a bit like this

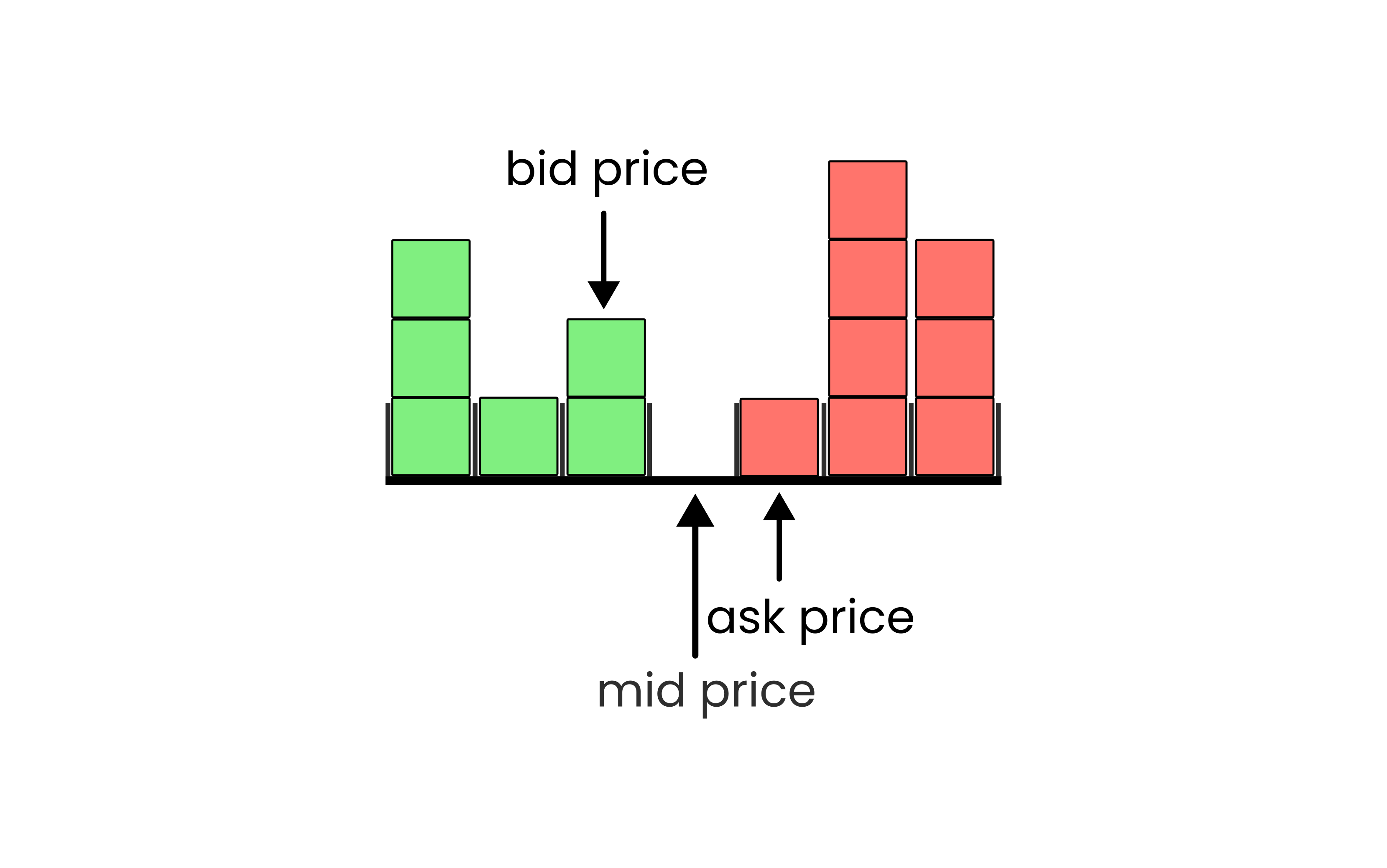
These buy orders and sell orders are kept either somebody submits what’s called a “market order” or the trader that placed the order cancels it. A market order is an order that effectively asks to buy or sell at the best price available no matter what it is. For example, if the order book for a stock has two ask orders both with quantity 1 at $194 and $195 for one stock then if I submit a market order to buy this stock then the exchange would match me with the $194 ask order from the order book and we would trade at this price: I get the stock from the seller and the seller gets $194 from me. After this we’ve traded the ask order is removed from the order book since it only had quantity 1.

We call the difference between the most aggressive (highest) bid price and the most aggressive (lowest) ask price the bid-ask spread. Zero-intelligence models model the dynamics of the orderbook as a random process and even though they don’t model the individual behaviour of traders in the market according to Farmer et al. (2005) they are able to predict up to 95% of the variance in the bid-ask spread.

Typically we model the arrival of bid and ask orders as a Poisson process which looks like this as an SDE

\[dN_t = \begin{cases} 1 &\text{with probability } \lambda dt \\ 0 &\text{with probability } 1 - \lambda dt \end{cases} \]

In a basic model we can have independent poisson processes describing the arrival of bids ands asks for every possible price or “tick” so we’d have a poisson process describing the dynamics of $1 bids, $2 bids and so on. In this model we also use a poisson process to describe how bids and asks exit the order book. This is a basic queueing model called a birth-death process.

If we use \(\mu\) to refer to the rate at which orders leave our order book queues then we have the neat result that if \(\lambda < \mu\) then our queueing system has a time-invariant steady state distribution. This means that in the long run our queue doesn’t grow indefinitely and we has a statistical distribution that doesn’t change throughout time, namely a geometric distribution with parameter \(1 - \frac{\lambda}{\mu}\). Furthermore, we can actually characterise the behaviour of this queue with a parameter \(\rho = \frac{\lambda}{\mu}\) and our queue is stable if \(\lambda < \mu\) or \(\rho < 1\).

In a simple system we have a perfect market maker who maintains a spread of exactly one tick. In this system we have a flat order book with unit bids and asks at every tick above the midprice and after a market order comes in and clears a limit order the dealer will place a bid to maintain the spread of 1 tick. However there are two ways of doing this: the the dealer can either submit a limit order on the same side as the incoming market order or on the opposite side. If we call the probability that the dealer places a limit orde on the same side as the market order \(u\) then we can model the midprice directly with an SDE.

Using \(P\) to denote the midprice, \( N_t^{\text{buy}} \sim \operatorname{Poisson}(\gamma^{\text{buy}})\) and \(N_t^{\text{sell}} \sim \operatorname{Poisson}(\gamma^\text{sell})\) to denote the poisson processes describing the incoming market buy orders and the market sell orders respectively, \(\Delta P\) to denote the smallest increment in price and \(Z \sim \operatorname{Bernoulli}(u)\) to represent the Bernoulli distributed random variable denoting which side the market maker places their limit order then we get the following SDE describing the dynamics of the mid price.

\[ dP = \Delta P (dN^{\text{buy}}_t - dN^{\text{sell}}_t) Z \]

Now, using a little bit of functional analysis we can work out the infinitesimal generator for our system. The infinitesimal generator describes the evolution of our system over a small time frame. I found this lecture video helpful for getting a better idea of what the infinitesimal generator is and also this lecture that walks through the derivation of the infinitesimal generator for a Poisson process. By definition, our infinitesimal generator looks like this

\[ \begin{align*} \mathcal{L}_f(p) &= \lim_{t \to 0^+} \frac{\mathbb E \left[ \left. f(P_t) \right| P_0 = p \right] - f(p)}{t} \\ &= \lim_{t \to 0^+} \frac{\mathbb E \left[ \left. f(P_t) - f(p) \right| P_0 = p \right]}{t} \\ &= u \left( \gamma^{\text{buy}} \left(f(p + \Delta P) - f \right) + \gamma^{\text{sell}} \left( f(p - \Delta P) - f\right) \right) \\ &= \frac{1}{2}u\left( \gamma^{\text{buy}} + \gamma^{\text{sell}} \right)(\Delta p)^2 \frac{f(p + \Delta P) - 2f + f(p - \Delta P)}{\Delta P^2} \\ &+ u \left( \gamma^{\text{buy}} - \gamma^{\text{sell}} \right) \Delta P \frac{f(p + \Delta P) - f(p - \Delta P)}{2\Delta P} \end{align*} \]

The final equality is a trick from Gould et al. (2013), the textbook I’m learning from. Combined with the assumptions that \( u\left( \gamma^{\text{buy}} + \gamma^{\text{sell}} \right)\) tends to \(\sigma^2\) and \(u \left( \gamma^{\text{buy}} - \gamma^{\text{sell}} \right) \Delta P\) tends to \(\mu\) as the smallest tick price increment becomes arbitrarily small, this allows us to rewrite our generator as

\[ \frac{\sigma^2}{2}\frac{\partial f}{\partial p^2} + \mu \frac{\partial f}{\partial p} \]

This corresponds to the the generator for brownian motion with drift proportional to \(u \left( \gamma^{\text{buy}} - \gamma^{\text{sell}} \right)\). So in this basic model we find that the midprice is controlled by how the market maker interacts with the order book with the \(u\) parameter and also the difference in the arrival rates of market orders to buy and sell.

Taking a step back this makes sense: if \( \gamma^{\text{buy}} > \gamma^{\text{sell}} \) and on average there are more buy orders than sell orders then in this model then the drift will be positive and the price will go up when \(u > 0\). But what does \(u\) represent?

While I was learning about banking I learned about the Treynor model of the dealer in asset markets. In Treynor’s model the dealer is a profit-seeking agent who attempts to control risk by limiting their exposure to the asset or how long or short they are on the asset in question. In Treynor’s model, if the dealer is heavily long on a security then they will quote lower prices to encourage market participants to buy from the dealer, allowing the dealer sell and offload some of their holdings of the asset.

Using this idea, I think we can interpret \(u\) as representing how sensitive the dealer is to market pressure. When \(u\) is 1 then the dealer will place limit bid orders whenever seeing a market buy order which moves the price upwards in accordance to market demand. In Treynor’s model this corresponds to the dealer setting prices to help control their exposure to the asset that they’re trading.

There are more sophisticated models of the order book that are really interesting. I was watching a lecture by Frank Kelly describing a simple Markovian model of the order book that rendered some problems analytically tractable. In the lecture he shows how you can use this model to analyse the game-theoretic nash equilibrium market making strategies and how they change after introducing new policies or regulation.

Huang et al. (2015) introduce what they call the queue-reactive model where the rate at which orders arrive depend on the state of the order book which turns out to model the stationary state of the order book really well and closely match empirically observed market data from exchanges.

Learning about modelling order books was really interesting and it was fun seeing all the different approaches and comparing how they analyse order book dynamics. The appeareance of the infinitesimal generator was extremely surprising, my textbook assumed knowledge of it and didn’t spend any time introducing the idea or explaining how it works but learning about it was really cool and I found it really interesting how manipulating it revealed insights into the dynamics of the system that it modelled.

All in all, market microstructure models are really interesting.

References

[1]: Abergel, Frédéric, et al. Limit order books. Cambridge University Press, 2016.

[2]: Huang, Weibing, Charles-Albert Lehalle, and Mathieu Rosenbaum. “Simulating and analyzing order book data: The queue-reactive model.” Journal of the American Statistical Association 110.509 (2015): 107-122.

[3]: Kelly, Frank, and Elena Yudovina. “A Markov model of a limit order book: thresholds, recurrence, and trading strategies.” Mathematics of Operations Research 43.1 (2018): 181-203.

[4]: Hambly, Ben. “Introduction to Limit Order Book Markets”

[5]: Gould, Martin D., et al. “Limit order books.” Quantitative Finance 13.11 (2013): 1709-1742.

[6]: Farmer, J. Doyne, Paolo Patelli, and Ilija I. Zovko. “The predictive power of zero intelligence in financial markets.” Proceedings of the National Academy of Sciences 102.6 (2005): 2254-2259.

[7]: Harry Sapranidis Mantelos, “Limit Order Book Modeling”

[8]: Kelly, Frank, and Elena Yudovina. “A Markov model of a limit order book: thresholds, recurrence, and trading strategies.” Mathematics of Operations Research 43.1 (2018): 181-203.