Markov-Chain Monte Carlo algorithms for Bayesian inference
Implementing Metropolis-Hastings and Hamiltonian Monte Carlo in C++
26 December 2024
I’m going to write a bit about Markov Chain Monte Carlo, a class of algorithms that power large amounts of modern computational statistics.
Monte Carlo
When performing bayesian inference with complex models we often encounter statistical problems that we cannot solve analytically. For example, say that we’ve observed some data and we wanted to find the Bayes Estimator for our parameters given these observations. To get our estimates for our parameter we would need to take an expectation over the posterior distribution which is itself an integral expression over the posterior distribution.
Unfortunately we can seldom analytically solve for these outside for a few special cases since the posterior distribution often does not have a nice closed-form expression. As such, we find ourselves forced to turn to numerical methods to approximate the value of these integrals.
Monte Carlo methods are a class of algorithms that rely on random simulation and sampling to estimate the solution to problems. For example, we may use a simple Monte Carlo scheme to find the expected value of a distribution by sampling from the distribution and computing the sample average.
That is to say that we can make \(n\) observations, \(X_i\), drawn independently from the same distribution with expectation \(\mathbb E \left[ X_i \right] = \mu\) then we can approximate the expectation \(\mu\) by calculating the sample average which is just \(\frac{1}{n}\sum_{i=1}^n X_i\). As we take more and more samples the weak law of large numbers tells us that our sample average will get closer to the expectation.
We can also use this to take expectations over transformations of our distribution by taking the sample average of any function applied to the samples that we observe. For example, if we wanted to estimate the percentage of our distribution that falls below 5 then all we have to do is take the average of the indicator function applied to our sample. That would be \[I(x) = \begin{cases}1, & x < 5 \\ 0, & \text{otherwise} \end{cases}\]
For example, if our sample is \(\{1, 8, 10, 2, 2, 6, 7, 3, 4, 10 \}\) then the value of our indicator for this sample would then be \(\{1, 0, 0, 1, 1, 0, 0, 1, 1, 0\}\) which looks like this in a table.
| Sample value | Indicator value |
|---|---|
| 1 | 1 |
| 8 | 0 |
| 10 | 0 |
| 2 | 1 |
| 2 | 1 |
| 6 | 0 |
| 7 | 0 |
| 3 | 1 |
| 4 | 1 |
| 10 | 0 |
Averaging the values of the indicator function we estimate that 50% of our distribution falls below 5.
Markov Chains
Modern statistics tools use Monte Carlo methods based on Markov chains to perform Bayesian inference.
A stochastic process is a series of random observations indexed by time that come fom a set of states called the state space. For example, we could model the weather as stochastic process where we index our process by the date and our state space consists of the labels “sunny” and “rainy”.
Markov chains are stochastic processes where the probability of entering a new state only depends on what state you’re currently in. So if we built a Markov chain to model the weather in the same way then I could fully specify my model with 4 parameters:
- The probability it is sunny tomorrow given that it is sunny today
- The probability it is sunny tomorrow given that it is rainy today
- The probability it is rainy tomorrow given that is sunny today
- The probability it is rainy tomorrow given that is rainy today
There’s a bit of redundancy here since probabilities that partition our state space add up to 1 and we only actually need two parameters since we can infer the other two probabilities. That being said, we can represent this information in a matrix: if we use \(S_t\) to represent the event where it is sunny at time \(t\) and \(R_t\) to represent the event where it is rainy at time \(t\) we can represent our model as a matrix as so
\[ \begin{bmatrix} P(R_{t + 1} | R_t) & P(S_{t + 1} | R_t) \\ P(R_{t + 1} | S_t) & P(S_{t + 1} | S_t) \end{bmatrix} \]
If we give some values to these probabilities our transition matrix might look like this
\[ \begin{bmatrix} 0.6 & 0.4 \\ 0.2 & 0.8 \end{bmatrix} \]
We can graphically represent this with the following diagram
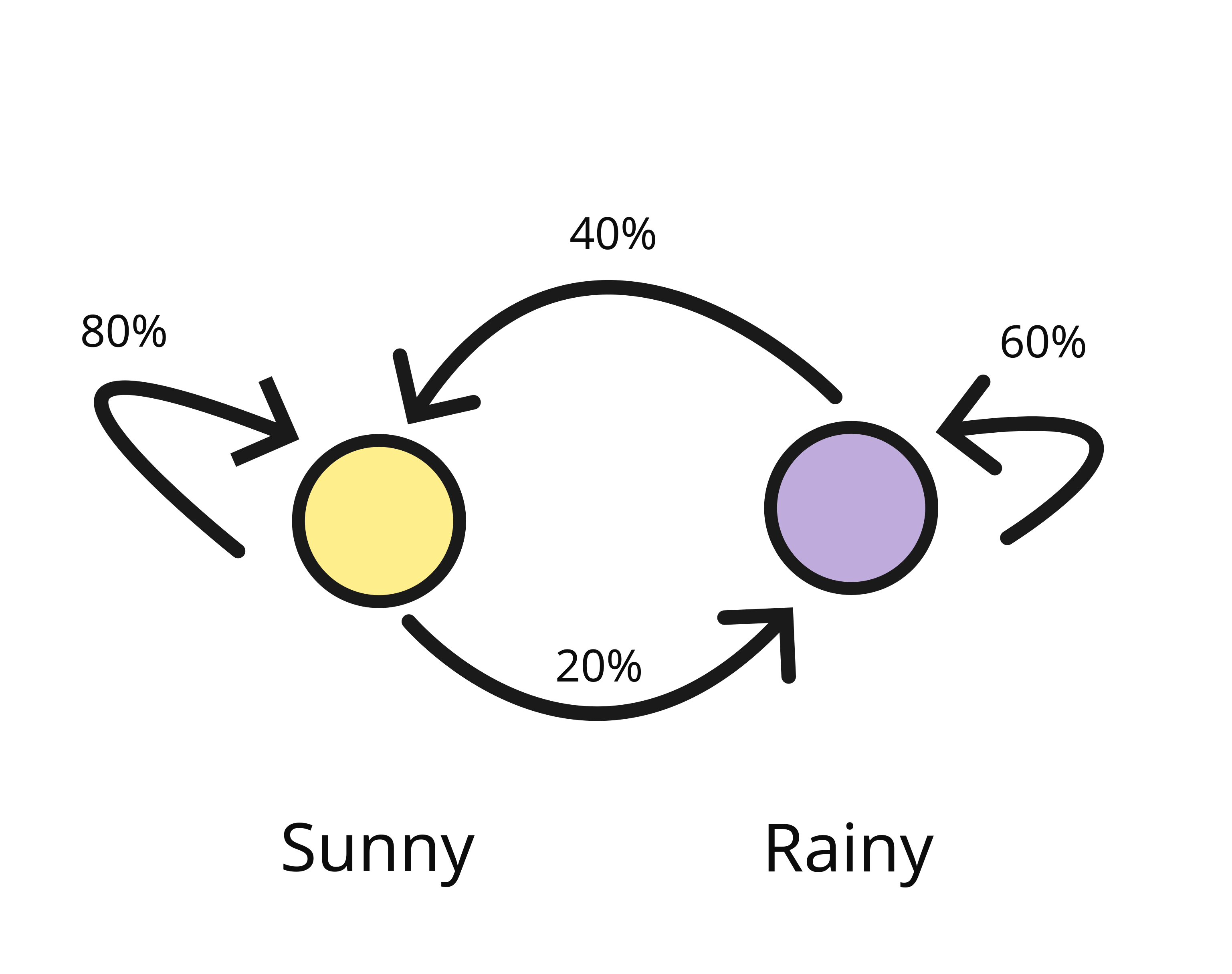
In the above diagram representation of our Markov Chain our cicles represent our states and the arrows represent the probability of transitioning to each state given our current state.
We can now start asking questions about the long-run behaviour of our system such as “if I start in the sunny state what does our distribution of states look like after 5 steps?”. If we use \(P^{(n)}_{i,j}\) to denote the probability of being in state \(j\) after \(n\) steps if we start in state \(i\) then if \(M\) is our transition matrix of probabilities then we have \(P^{(n)}_{i, j} = M^n_{i, j}\) where \(M^n\) is the nth power of our transition matrix and represents repeated matrix multiplication and we can prove this fact using induction.
One interesting property about the behaviour of Markov chains in the long run is that they tend to “forget” where they start from. For example let’s look at some powers of our matrix
\[ \begin{align*} M^0 &= \begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix} \\ M &= \begin{bmatrix} 0.6 & 0.4 \\ 0.2 & 0.8 \end{bmatrix} \\ M^2 &= \begin{bmatrix} 0.44 & 0.56 \\ 0.28 & 0.72 \end{bmatrix} \\ M^3 &= \begin{bmatrix} 0.38 & 0.62 \\ 0.31 & 0.69 \end{bmatrix} \\ M^{100} &= \begin{bmatrix} 0.33 & 0.67 \\ 0.33 & 0.67 \end{bmatrix} \\ \lim_{n \to \infty}M^n &= \begin{bmatrix} \frac{1}{3} & \frac{2}{3} \\ \frac{1}{3} & \frac{2}{3} \end{bmatrix} \end{align*} \]
All of our rows look exactly the same and our columns are filled with the same value, this is saying that after a larger number of steps it doesn’t actually matter where we start from: in the long run our distribution of states tends to be the same no matter where we begin.
More concretely, in the long run on arbitrary day we have a one in three chance of seeing a rainy day and a two in three chance of it being sunny. This distribution of states is called the stationary distribution and we can prove that this distribution always exists for a finite state space using the Krylov-Bogoliubov Argument.
Markov Chain Monte Carlo
As discussed earlier, in computational statistics we often want to sample from complex distributions. But what if we could construct a Markov chain whose stationary distribution matches the distribution we want to sample? If we’re able to do this then we can sample from our distribution by simply walking through our markov chain.
Before continuing, one thing that we should note is that our distribution is potentially infinite: instead of “sunny” and “rainy” the support of our distribution could span the entire real number line. Furthermore, we could have a multivariate distribution where our observations are many real numbers, not just one.
In probability there’s the concept of a reversible markov chain. A Markov chain is reversible if the process we get from reversing the transition probabilities (or flipping the arrows in the diagram) has the same statistical properties as the original Markov chain.
If we have a stationary Markov chain like our Markov chain representing the long-run behaviour of our weather model from earlier then if it’s reversible we have \(P(X_t = j, X_t = i) = P(X_t = i, X_t = j)\). If the long-run probability of being in state \(i\) is \(\pi(i)\) then this equality becomes \(\pi(i) P(X_t = j | X_t = i) = \pi(j) P(X_t = i | X_t = j)\). This equality is called the detailed balance equation and any such \(\pi\) that satisfies this detailed balance equation must be a stationary distribution for our Markov chain. This is really powerful and it allows us to create a Markov chain for any distribution \(\pi\).
Let \(\pi\) be the distribution we want to sample from then if we let \(q_{i,j}\) be any Markov chain on out state space with non-zero probabilities such that \(q_{i,j} = q_{j, i}\) then we can construct a Markov chain \(p_{i, j}\)
\[ \begin{align*} p_{i, j} &= \min\left(q_{i, j}, \frac{\pi_j q_{j, i}}{\pi_i} \right) \\ p_{i, i} &= 1 - \sum_{j \neq i} p_{i, j} \end{align*} \]
We can interpret \(q_{i, j}\) as a “proposal” distribution that suggests where to explore in the sample space, then we use the actual distribution we want to sample from \(\pi\) to accept or reject this proposal.
Now for \(i \neq j\) we have
\[ \begin{align*} \pi_ip_{i, j} &= \pi_i \min\left(q_{i, j}, \frac{\pi_j q_{j, i}}{\pi_i} \right) \\ &= \min\left(\pi_i q_{i, j}, \pi_j q_{j, i} \right) \\ &= \pi_i q_{i, j} \end{align*} \]
As per the theorem this proves that \(\pi\) is the stationary distribution of this Markov chain we constructed and that is the essence of the Metropolis-Hastings algorithm. In order to sample from our distribution all we have to do is simulate this Markov chain that we’ve constructed and the only requirements that we have on \(q\) are non-zero probabilities and an equal probability of getting to \(j\) from \(i\) and to \(i\) from \(j\).
The Metropolis-Hastings algorithm
Putting all of these together we form the basis for a basic Monte Carlo sampling algorithm. The algorithm generalises for to distributions of any dimension but for simplicity I stick to the one dimensional case. I used a standard normal distribution for my proposal distribution with \(\epsilon \sim \mathcal{N}(0, 1)\) and \(q_{i, j} = p_\epsilon(j - i))\) My implementation in C++ looks like this
#include <cmath>
#include <functional>
#include <iostream>
#include <random>
const int BURN_IN = 10'000;
const int EXPECTATION_SAMPLE_SIZE = 100'000;
template <auto pdf> class RandomWalkMetropolis {
std::default_random_engine generator{};
std::normal_distribution<float> step_sampler;
std::uniform_real_distribution<float> uniform_sampler;
float x{};
public:
RandomWalkMetropolis() : step_sampler(0, 1), uniform_sampler(0, 1) {}
void initialise() {
for (int i = 0; i < BURN_IN; ++i) {
sample();
}
}
float sample() {
float dx = step_sampler(generator);
float proposal = x + dx;
float ratio = pdf(proposal) / pdf(x);
if (uniform_sampler(generator) < ratio) {
x = proposal;
}
return x;
}
float expectation(std::function<float(float)> f) {
float total{};
for (int i = 0; i < EXPECTATION_SAMPLE_SIZE; ++i) {
total += f(sample());
}
return total / EXPECTATION_SAMPLE_SIZE;
}
};
// Exponential distribution pdf
float exponential(float x) {
if (x < 0) {
return 0;
}
return std::exp(-x);
}
float g(float x) { return std::pow(2, x); }
int main() {
float x = 0;
RandomWalkMetropolis<exponential> sampler{};
sampler.initialise();
std::cout << sampler.expectation(g);
}When run, the code outputs an approximation of \(\mathbb E_{x \sim \operatorname{Exp}(1)} \left[2^x\right] = \int_{0}^{\infty} e^{-x} 2^x\).
The Hamiltonian Monte Carlo algorithm
The Metropolist-Hastings algorithm works really well given how simple it is. However, it has some drawbacks. The first is that our performance depends on our “proposal” distribution \(q\). While asymptotically the Metropolist algorithm will give us good approximations, in the short-run if our targret distribution has small regions of very high probability density then we may miss these regions during the proposal step or get stuck inside them during our sampling process, biasing our estimate.
Furthermore, our areas with high expectation take up a smaller proportion of our proposal space as we scale upwards towards higher dimensions making them harder to find since there are an exponential number of directions that we could explore.
Hamiltonian Monte Carlo attempts to remedy this by tuning the proposal distirbution to take into account gradient information from the target distribution. Hamiltonian Monte Carlo is based on ideas from statistical mechanics and we imagine that our proposal is a partical in a physical system that has “momentum” so alongisde our proposal \(\mathbf q\) we also have a momentum \(\mathbf p\) and the partial derivatives of the Hamiltonian tell us how our particle moves through space and how its momentum changes. These equations look like this
\[ \begin{align*} \frac{d\mathbf q}{dt} &= \frac{\partial H}{\partial \mathbf p} \\ \frac{d\mathbf p}{dt} &= - \frac{\partial H}{\partial \mathbf q} \end{align*} \]
What’s useful about Hamiltonian mechanics is that it describes a reversible process since not only can we tell where our particle will be at any point in time given its startling location and momentum but we can also find out where our particle came from, going backwards in time. This reversisibility allows us to use it for MCMC.
Hamiltonian Monte Carlo works by converting our distribution’s density function to a potential energy function which we put into the Boltzman distribution to get the probability of our particle being at a certain position.
The Boltzman distribution assigns probability a probability density proportional to \(e^{\frac{E}{kT}}\) where \(E\) is the total energy of the system, \(k\) is the Boltzman constant and \(T\) is the temperature. The toal energy in our system is the hamiltonian so we get \(p(\mathbf q, \mathbf p) \propto e^{\frac{H(q, p)}{kT}}\) and we can numerically solve for H using the leapfrog algorithm algorithm.
My simplified implementation of the Hamiltonian Monte Carlo algorithm looks like this
#include <cmath>
#include <functional>
#include <iostream>
#include <random>
const float EPSILON = 0.01;
const int STEPS = 100;
const int EXPECTATION_STEPS = 100'000;
const int BURN_IN = 1'000;
template <typename Distribution> class HamiltonianMC {
float x{};
std::default_random_engine generator;
std::normal_distribution<float> momentum_sampler;
std::uniform_real_distribution<float> uniform_sampler;
Distribution distribution;
public:
HamiltonianMC() : momentum_sampler(0, 1), uniform_sampler(0, 1) {}
void initialise() {
for (int i = 0; i < BURN_IN; ++i) {
sample();
}
}
float sample() {
float proposal = x;
float initial_momentum = momentum_sampler(generator);
float momentum = initial_momentum;
for (int i = 0; i < STEPS; ++i) {
proposal += momentum * EPSILON;
momentum += EPSILON * distribution.logpdf_derivative(proposal);
}
float density_ratio = distribution.pdf(proposal) / distribution.pdf(x);
float kinetic_ratio = std::exp(std::pow(initial_momentum / momentum, 2));
if (uniform_sampler(generator) < density_ratio * kinetic_ratio) {
x = proposal;
}
return x;
}
float expectation(std::function<float(float)> f) {
float total{};
for (int i = 0; i < EXPECTATION_STEPS; ++i) {
total += f(sample());
}
return total / EXPECTATION_STEPS;
}
};
class Exponential {
public:
Exponential() {}
float pdf(float x) {
if (x <= 0)
return 0;
return std::exp(-x);
}
float logpdf(float x) { return -x; }
float logpdf_derivative(float x) { return -1; }
};
float f(float x) { return std::pow(2, x); }
int main() {
HamiltonianMC<Exponential> sampler{};
sampler.initialise();
std::cout << sampler.expectation(f) << std::endl;
}In my simplified code I used Euler’s method for numerical integration whereas moden implementations typically use leapfrog integration. Modern implementations use No-U-Turn Sampling or NUTS introduced by Hoffman and Gelman in a paper titled The No-U-Turn Sampler: Adaptively Setting Path Lengths in Hamiltonian Monte Carlo in 2011. The NUTS algorithm automatically tunes the number of steps taken during the leapfrog itegration phase of the algoirthm.
All in all I find it pretty cool how thermodynamics, statistical mechanics and Hamiltonian mechanics have found its way into sampling algorithms. It was a shock for me since I wasn’t familiar with physics let alone thermodynamics but I’m really happy that by learning about this I’ve gained a better understanding of modern day MCMC sampling algorithms and a tiny bit of physics and numerical methods too.
References
[1]: Turkman, M. Antónia Amaral, Carlos Daniel Paulino, and Peter Müller. Computational Bayesian statistics: an introduction. Vol. 11. Cambridge University Press, 2019.
[2]: Betancourt, Michael. “A conceptual introduction to Hamiltonian Monte Carlo.”
[3]: Kelly, Frank P. Reversibility and stochastic networks. Cambridge University Press, 2011.
[4]: Neal, Radford M. “MCMC using Hamiltonian dynamics.”
[5]: Hoffman, Matthew D., and Andrew Gelman. “The No-U-Turn sampler: adaptively setting path lengths in Hamiltonian Monte Carlo.” J. Mach. Learn. Res. 15.1 (2014): 1593-1623.