Benchmarking my perception of sound

15 December 2024

Learning about Bayesian statistics and the Jeffreys prior


I’ve been learning about Bayesian statistics and computational methods recently so I want to work on a few small projects to put into practice what I have been learning.

Today I decided to benchmark my perception of sound: I created a game where I’m played a random tone and I have to respond with a number that is as close as possible to the frequency that was played. I sample frequencies uniformly at random between 131Hz and 495Hz.

I wanted to do this experiment as I came up for two models for how I’d perform on this game. If we let YY be the frequency I report and XX be the frequency that I actually heard, my first model is that I will give the frequency that I heard added to some normally distributed error term, that is

Yi=Xi+ϵiY_i = X_i + \epsilon_i

Where ϵi∼N(μ,σ2)\epsilon_i \sim \mathcal{N}(\mu, \sigma^2). If this is the case, I’d expect μ\mu to be zero as I don’t expect to have a consistent bias to guessing higher or lower than the actual frequency.

My second model is motivated by the fact that human sound perception is inherently logarithmic and musical intervals are actually frequency ratios. For example, playing C3 then E3 sounds the same as playing a C4 then E4: it’s just an octave higher however the difference between C3 and E3 is about 35Hz and the difference between C4 and E4 is about 70Hz. And in fact, an octave difference is a doubling of the frequency not a fixed difference in Hz. My second model hypothesises that the differences between the logarithms of the frequencies or “cents” is normally distributed.

log⁡Yi=log⁡Xi+ϵi \log Y_i = \log X_i + \epsilon_i

Where ϵi\epsilon_i is again a normally distributed error term.

I decided to test these two models as I hypothesised that my absolute error in frequency would become worse for higher tones which is a consequence of the second model but not the first model. This came about as earlier this week, I began teaching myself to report numerical frequencies as opposed to the musical note names: I wanted to teach myself to respond with “440 Hertz” as opposed to “A4” in response to hearing a tone played at 440Hz.

I quickly created a python script to collect this data. It looks like this 

import pysine
import random

LOWEST = 131
HIGHEST = 494
should_continue = True
played = []
heard = []
iteration = 0
try:
    while should_continue:
        iteration += 1
        tone = LOWEST + random.random() * (HIGHEST - LOWEST)
        read = None
        while read is None:
            pysine.sine(tone)
            entered = input(f"{iteration}>> ").lower().strip()
            if entered == "q":
                should_continue = False
                break
            if entered == "r":
                continue
            try:
                read = float(entered)
            except:
                print("Unable to read number")
        print(f"Played {tone}, you heard {read}")
        played.append(tone)
        heard.append(read)
except KeyboardInterrupt:
    pass
except EOFError:
    pass

print("tone,heard")
for x, y in zip(played, heard):
    print(f"{x},{y}")

Here are the results from my first play through of the game where I answered 20 questions

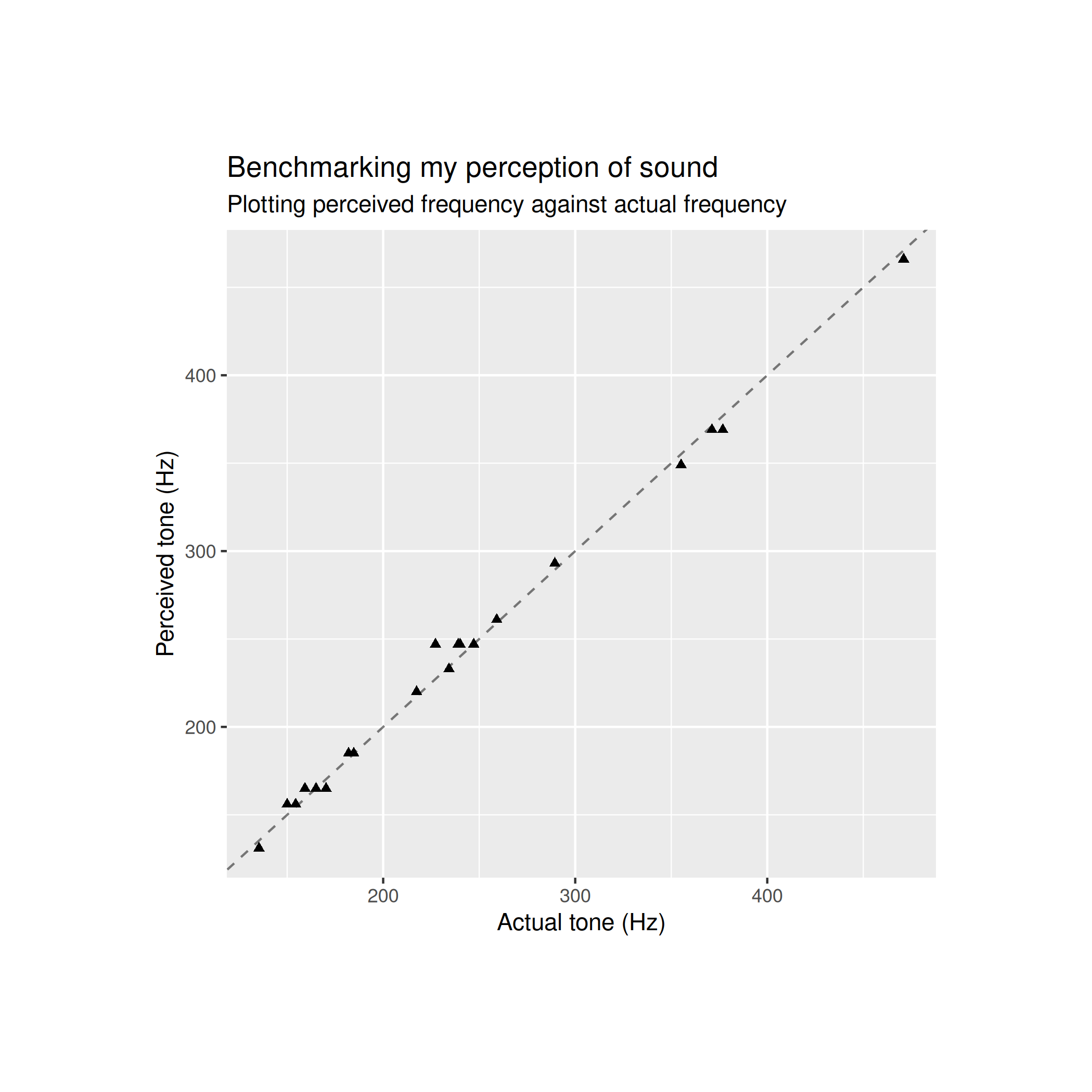
From a glance both of these models seem fairly sensible: my reported frequency appears to closely track the frequency that I actually heard. The error plot for my first game looks like this

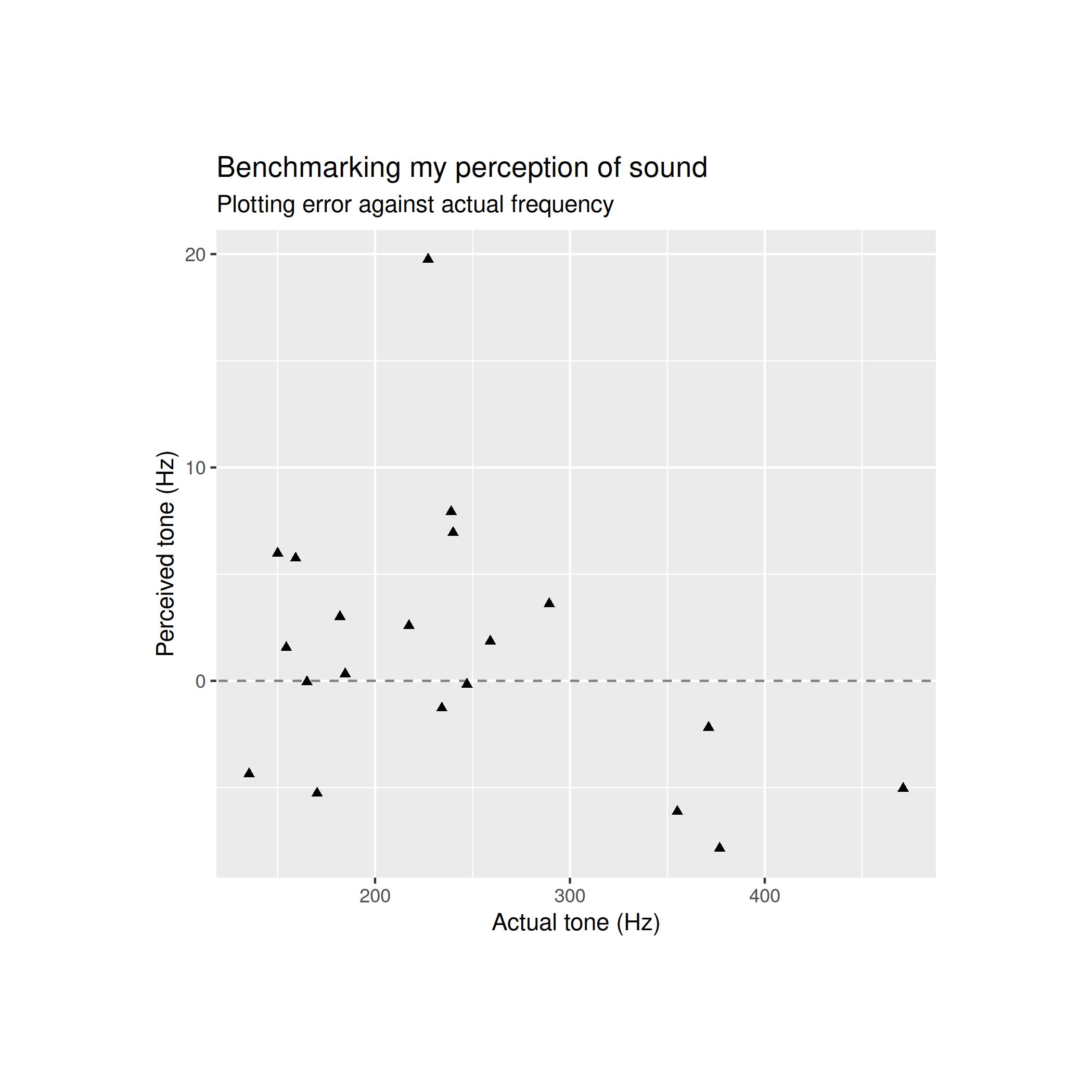
It’s hard to get any insights from this by just analysing the data visually, so I turn to statistics to compare how well these models explain the data.

The first thing I do is play another round of the game but this time I listen to 50 tones instead of just 20. The sine waves were also pretty boring to listen to so I synthesised my own instrument however I did a quick runthrough of the game with the synthesiser I made and I noticed that there was a clear upwards bias in the frequency that I reported. I reverted back to using sine waves and noticed that this bias disappeared which indicates that this bias was an artefact of how I wrote my synthesiser. I added harmonics but not subharmonics to my synth so this may have caused me to perceive the notes from the synthesiser as being higher than they actually were. That’s the euphemistic way of explaining that I wrote a bad synth.

After going back to using sine waves, the data I’m analysing looks like this

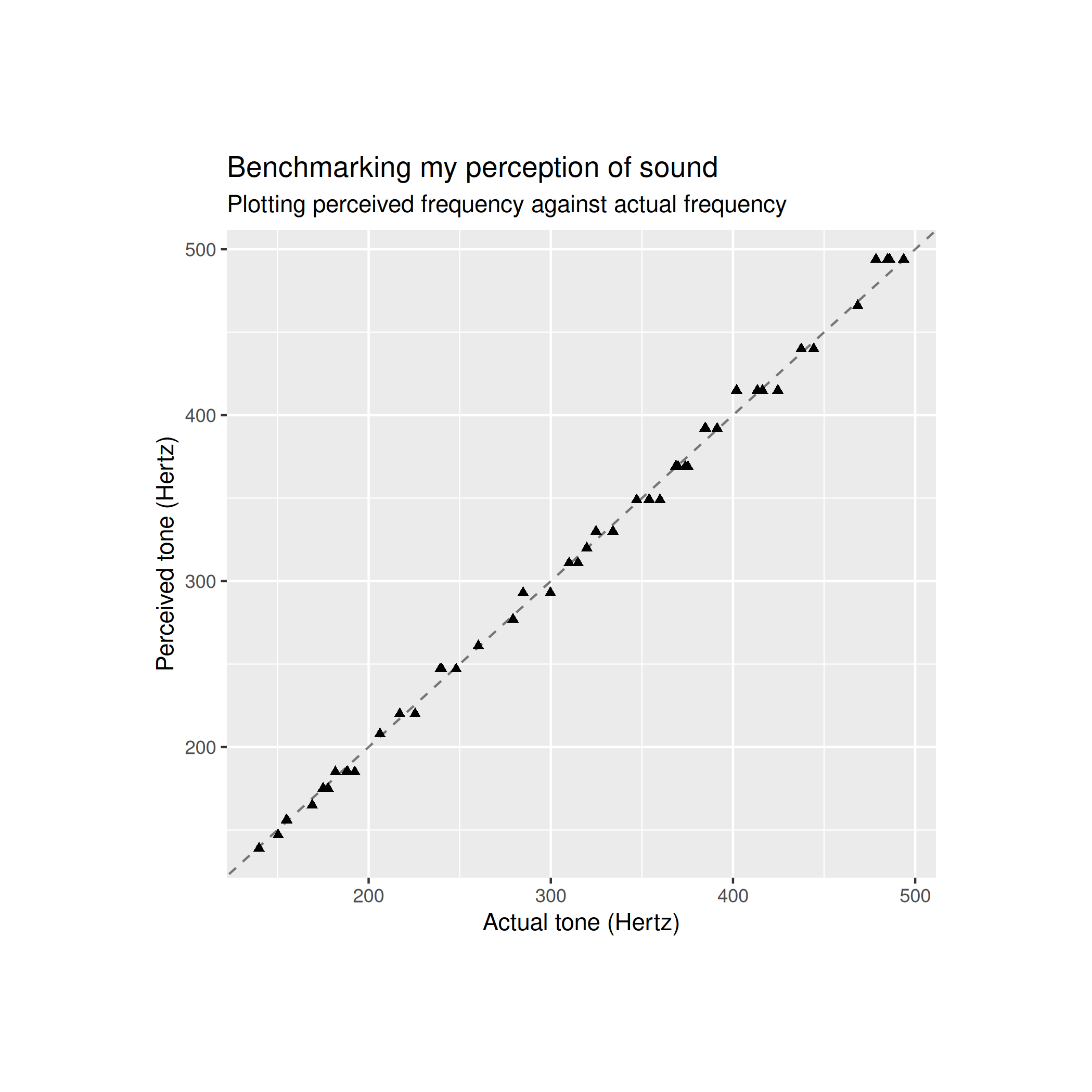
The error looks like this

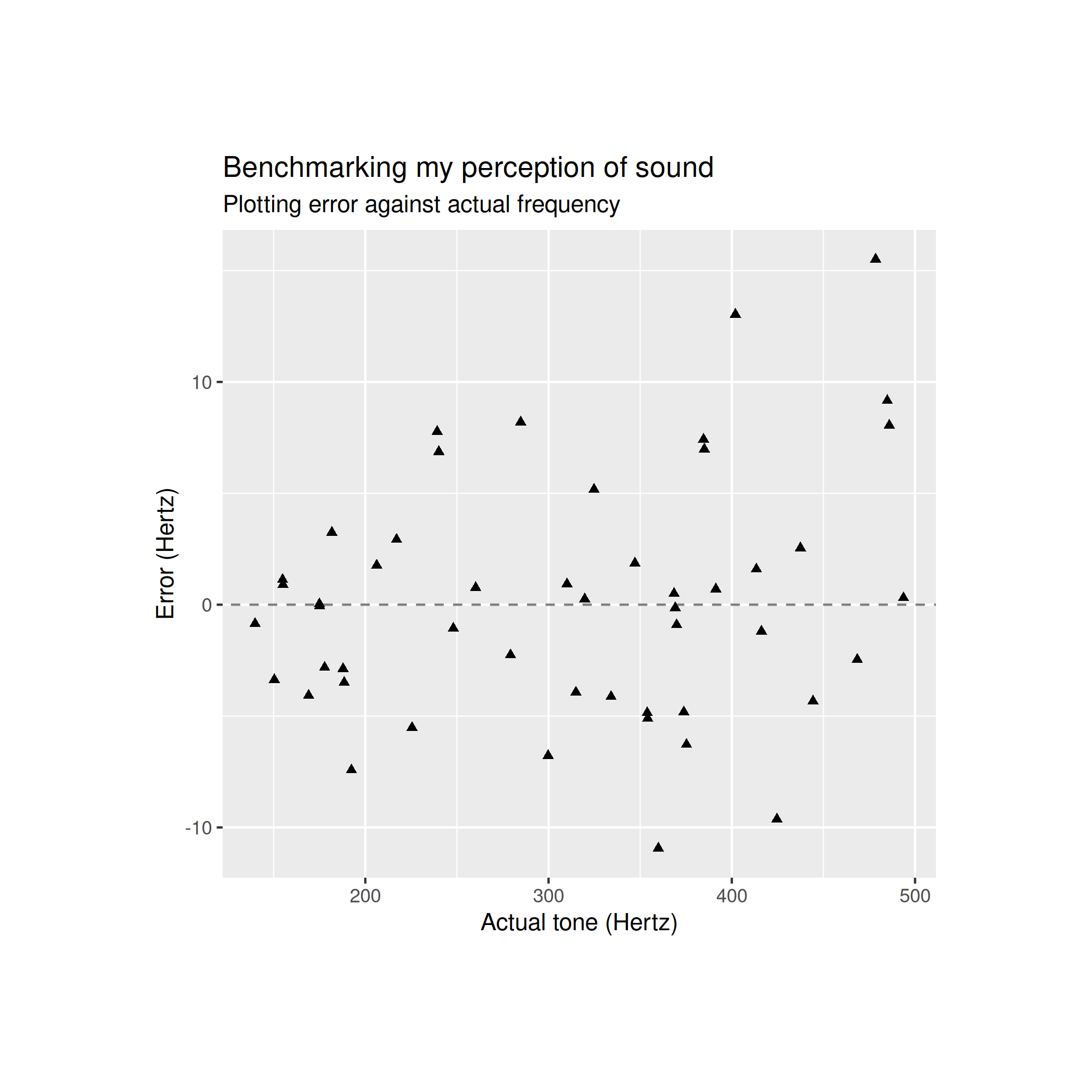
Now, the absolute error looks like this

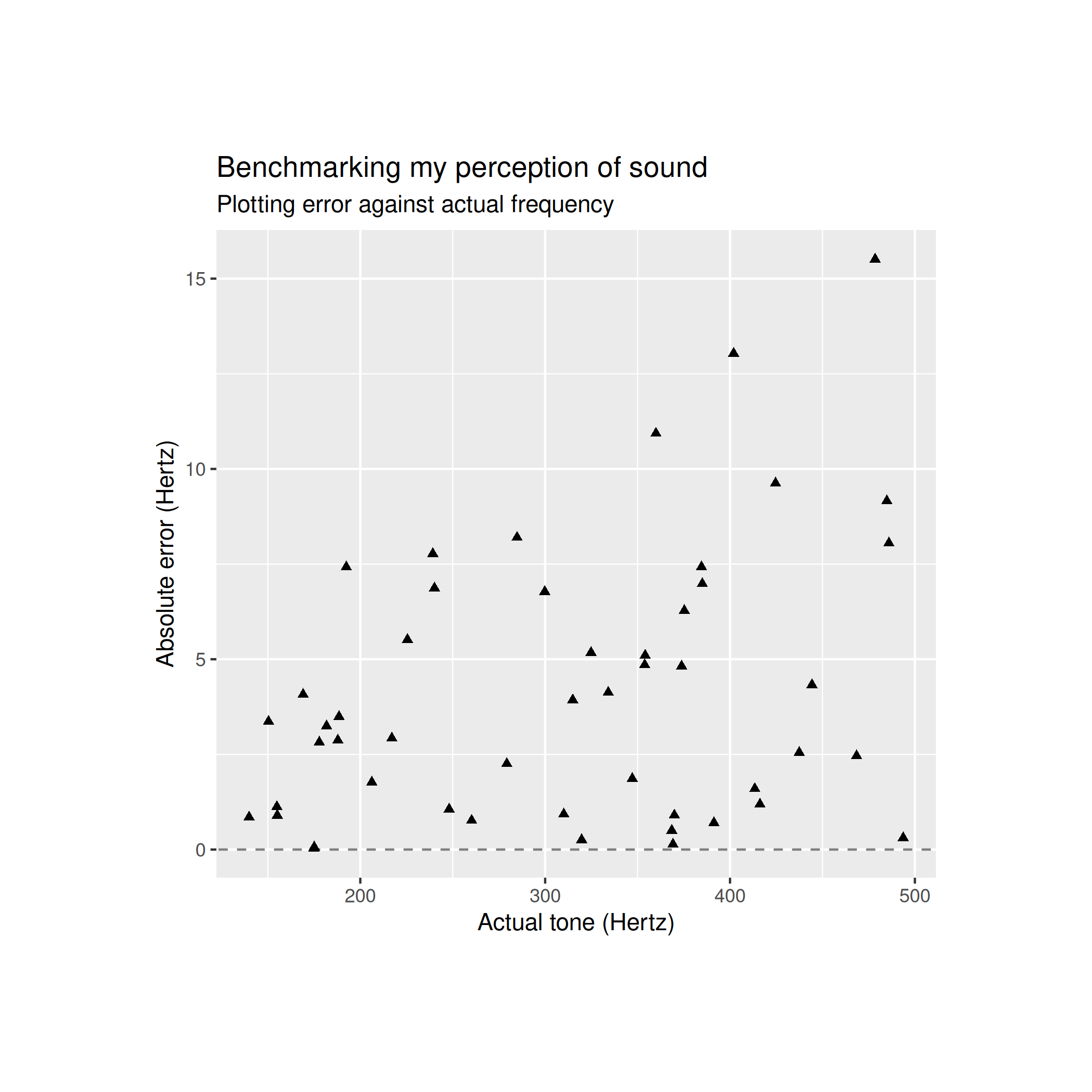
This final graph is important as it shows that the error term is clearly heteroskedastic which means that the variance of the error term is not constant: the error term has much larger variance for higher frequencies.

This matters because the first model predicts a homoskedastic resdiual term which does not match the data. My second model predicts heteroskedasticity but also predicts that the error for log frequency is homoskedastic. The plot for the absolute error between log frequencies looks like this

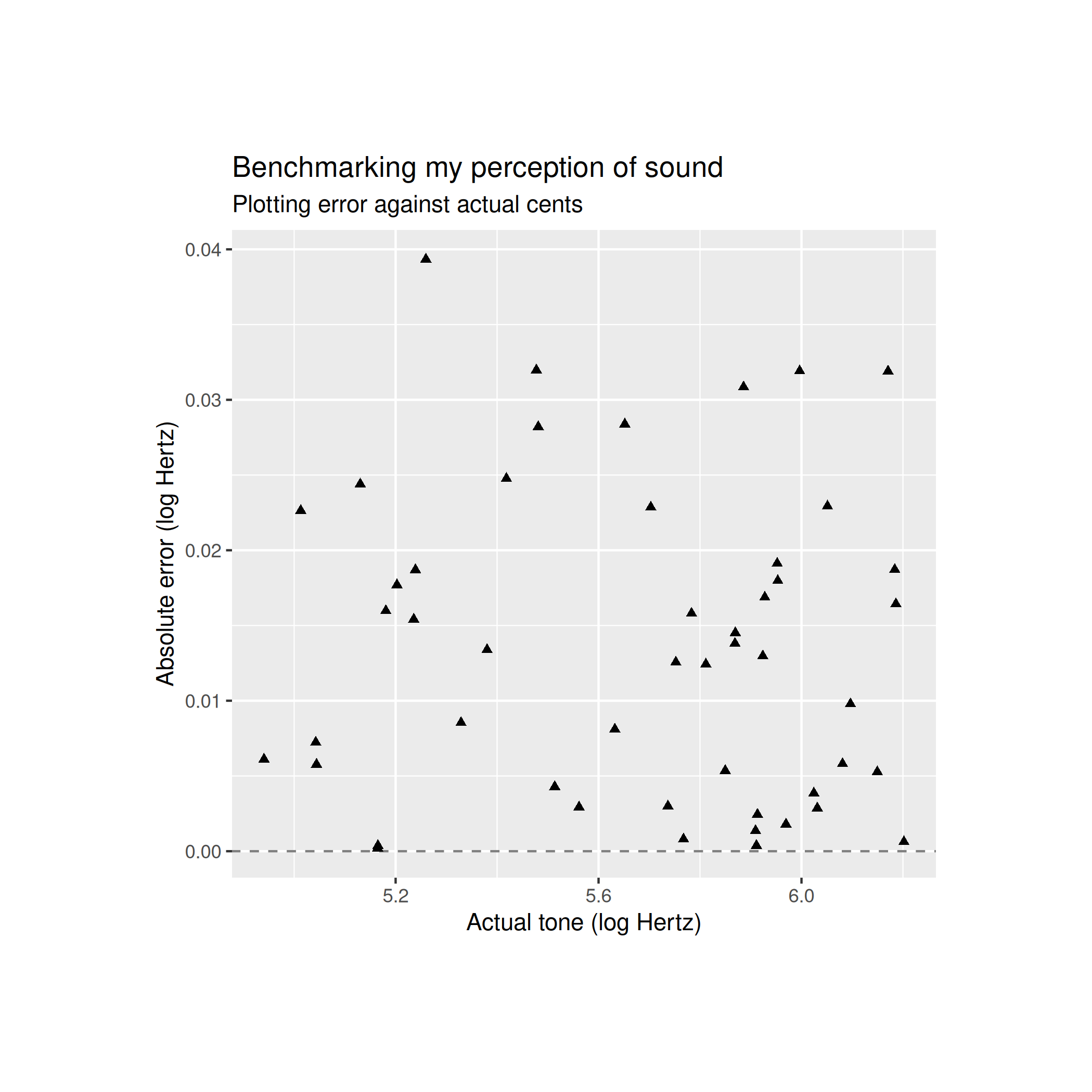
Visually, this is homoskedastic which is really good for the second model and is strong evidence that the second model better explains the data. Now, let’s quantitatively examine these models using bayesian statistics.

Bayesian statistics centres itself around Bayes’ rule which states that p(θ∣x)∝p(x∣θ)×p(θ)p(\theta | x) \propto p(x | \theta) \times p(\theta) or that the likelihood of θ\theta after having observed xx is proportional to the prior likelihood of theta multiplied by the probability of observing xx with parameter θ\theta.

What does this mean? If we have a distribution representing our beliefs about the value of θ\theta, Bayes’ rule tells us how to update our beliefs after observing new data. The distribution from before observing the data is called our “prior” and the updated distirbution after observing the data is called the “posterior”.

If we fix μ=0\mu = 0 for both models then both models become single paramter models as we have ϵi∼N(0,σ2)\epsilon_i \sim \mathcal{N}(0, \sigma^2). What is my prior distribution for σ\sigma?

For the sake of learning I’d like to use an uninformative prior: specifically, the Jeffreys prior, named after Harold Jeffreys.

The Jeffreys prior gives us a prior distribution that is invariant under montone transformations of the parameter. For example, if I took a uniform distribution as my prior for σ2\sigma^2 between 0 and 1 then the implied distribution of σ\sigma would also be between 0 and 1 but it would not be uniform. We can contrast this to the Jeffreys prior where the Jeffreys prior for σ2\sigma^2 aligns with the Jeffreys prior for σ\sigma.

The Jeffrey’s prior is specified as proportional to the square root of the determinant of the Fisher information matrix.

p(θ)∝det⁡I(θ) p(\theta) \propto \sqrt{\operatorname{det} \mathcal{I}(\theta)}

Our normal distribution with mean 0 looks like

f(x;σ)=12πσ2e−x22σ2 f(x ; \sigma) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{x^2}{2\sigma^2}}

We have a single parameter model so we get

p(σ)∝E[(∂∂σlog⁡f(x;σ))2∣σ]=E[(∂∂σlog⁡12πσ2e−x22σ2)2]=E[(∂∂σlog⁡e−x22σ2−log⁡2πσ2)2]=E[(∂∂σ−x22σ2−log⁡σ−12log⁡2π)2]=E[(∂∂σ−x22σ2−log⁡σ)2]=E[(x2σ3−1σ)2]=1σ2E[(x2σ2−1)2]∝1σ2=1σ \begin{align*} p(\sigma) &\propto \sqrt{\mathbb E \left[ \left. \left( \frac{\partial}{\partial \sigma} \log f(x;\sigma) \right)^2 \right| \sigma \right]} \\ &= \sqrt{\mathbb E \left[ \left( \frac{\partial}{\partial \sigma} \log \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{x^2}{2\sigma^2}} \right)^2 \right]} \\ &= \sqrt{\mathbb E \left[ \left( \frac{\partial}{\partial \sigma} \log e^{-\frac{x^2}{2\sigma^2}} - \log \sqrt{2\pi\sigma^2} \right)^2 \right]} \\ &= \sqrt{\mathbb E \left[ \left( \frac{\partial}{\partial \sigma} - \frac{x^2}{2\sigma^2} - \log \sigma - \frac{1}{2} \log 2\pi \right)^2 \right]} \\ &= \sqrt{\mathbb E \left[ \left( \frac{\partial}{\partial \sigma} -\frac{x^2}{2\sigma^2} - \log \sigma \right)^2 \right]} \\ &= \sqrt{\mathbb E \left[\left( \frac{x^2}{\sigma^{3}} - \frac{1}{\sigma} \right)^2 \right]} \\ &= \sqrt{\frac{1}{\sigma^2} \mathbb E \left[\left( \frac{x^2}{\sigma^2} - 1 \right)^2 \right] } \\ &\propto \sqrt{\frac{1}{\sigma^2} } \\ &= \frac{1}{\sigma} \end{align*}

Unfortunately, this is an improper prior and the integral across the support is not finite and does not form a true probability distribution. I’m too scared to use an improper prior after reading about how they can lead to nonsense inference results. Analysing whether or not they’re appropriate to use appears to be very complicated so I’ll stay away from improper priors for a few years.

Fortunately, I can create my own uninformative prior. I want to feign ignorance about both the variance and the standard deviation so I’d like a prior that ensures me transformational invariance between σ\sigma and σ2\sigma^2 I can get this with any pair of distributions fσf_{\sigma} and fσ2f_{\sigma^2} that satisfy

fσ(x)=dx2dxfσ2(x)=2xfσ2(x) \begin{align*} f_{\sigma}(x) &= \frac{dx^2}{dx} f_{\sigma^2}(x) \\ &= 2xf_{\sigma^2}(x) \end{align*}

So we now have

∫a∞fσ2(x)dx=∫a∞fσ(x)dx∫a∞fσ2(x)dx=∫a∞2xfσ2(x)dx∫a∞fσ2(x)(1−2x)dx=0 \begin{align*} \int_a^{\infty} f_{\sigma^2}(x) dx &= \int_a^\infty f_{\sigma}(x) dx \\ \int_a^{\infty} f_{\sigma^2}(x) dx &= \int_a^\infty 2xf_{\sigma^2}(x) dx \\ \int_a^{\infty} f_{\sigma^2}(x) \left( 1 - 2x \right) dx &= 0 \end{align*}

Integrating this by parts we get

∫a∞fσ2(x)(1−2x)dx=0−fσ2(0)+2∫a∞Fσ2(x)dx=02∫a∞Fσ2(x)dx=fσ2(a)2E[σ2]dx=fσ2(a) \begin{align*} \int_a^{\infty} f_{\sigma^2}(x) \left( 1 - 2x \right) dx &= 0 \\ -f_{\sigma^2}(0) + 2 \int_a^\infty F_{\sigma^2}(x) dx &= 0 \\ 2 \int_a^\infty F_{\sigma^2}(x) dx &= f_{\sigma^2}(a) \\ 2 \mathbb E\left[\sigma^2\right] dx &= f_{\sigma^2}(a) \end{align*}

Where Fσ2F_{\sigma^2} denotes the CDF for fσ2f_{\sigma^2} and aa lower bounds the variance in this distribution. Unfortunately, I do not want to solve this functional equation so I’ll just use the Jeffreys prior.

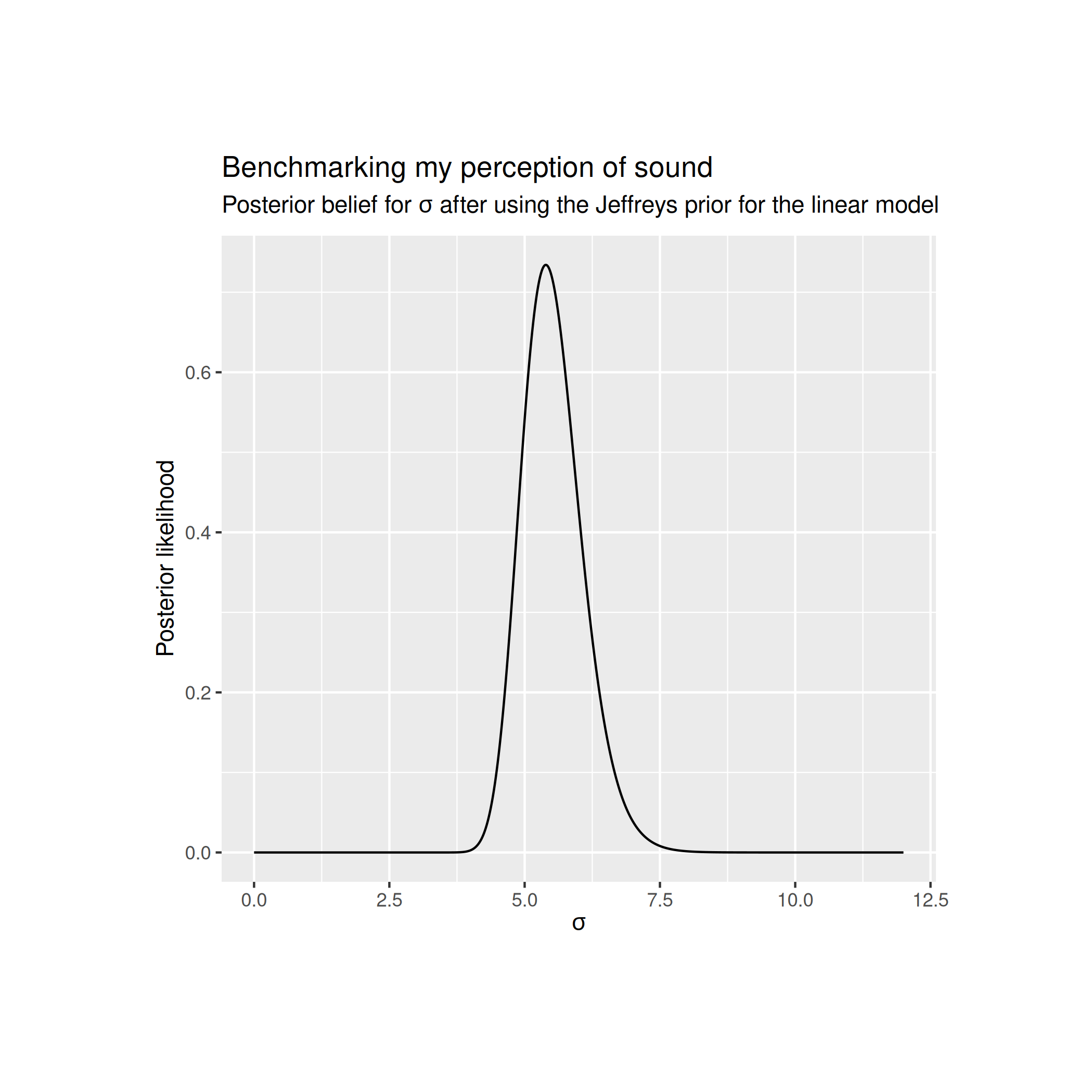
Using the Jeffreys prior for the linear model gives me the following posterior distribution

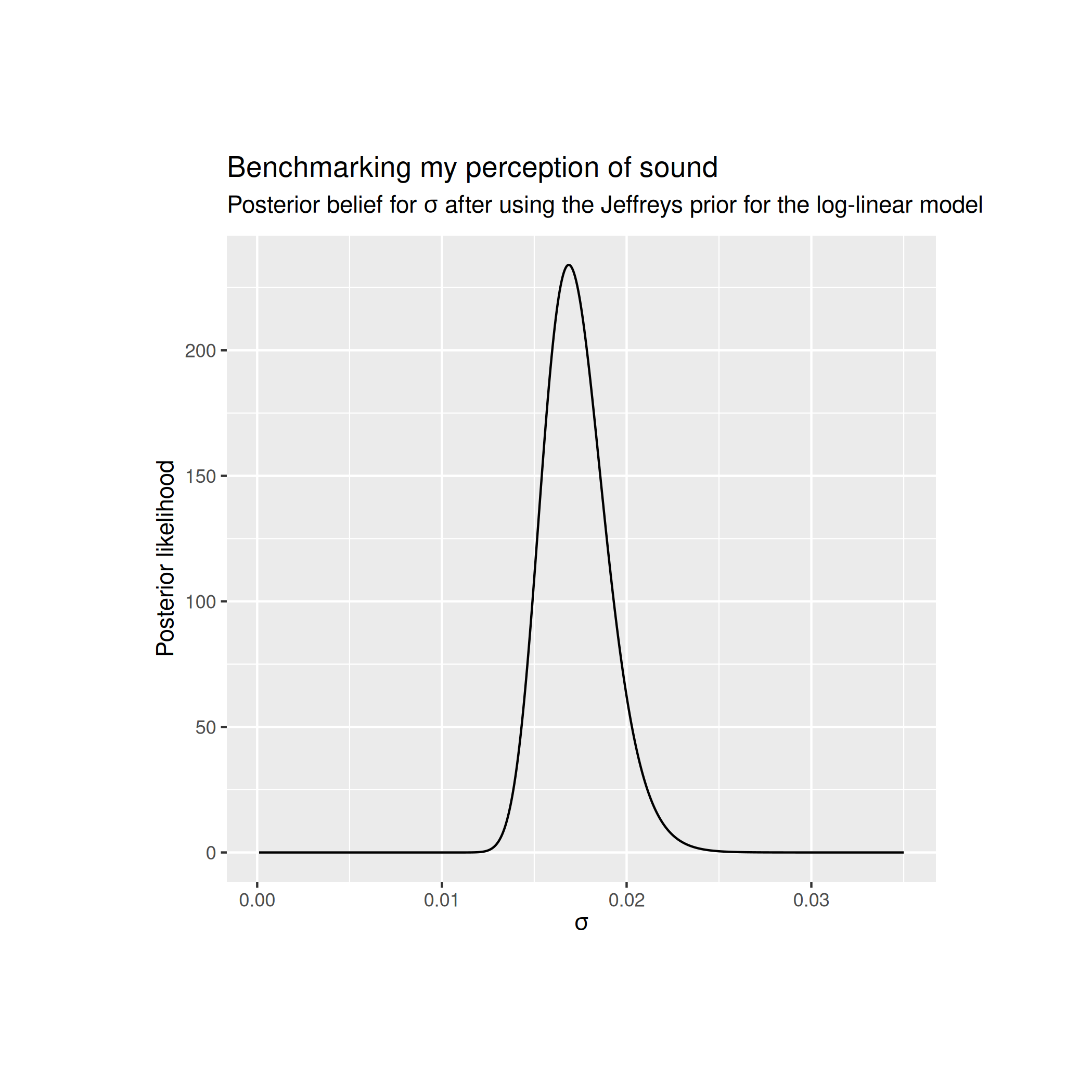
The Jeffreys prior for the log-linear model gives me the following posterior distribution

After taking the MLE for each of these models I can find a point estimate for the Bayes factor for the two models. The Bayes factor allows me to quantify how much better one model explains the data than another.

My code for calculating the likelihoods for each of the models looks like this 


likelihood_linear <- prod(dnorm(df$heard - df$tone, mean=0, sd=sigma_linear))
likelihood_log <- prod(dnorm(log(df$heard) - log(df$tone), mean=0, sd=sigma_log))
likelihood_log / likelihood_linear

The likelihood for the the first model is about 10−6810^{-68} whereas the likelihood for the second model comes out to be around 105910^{59}. This gives us a ratio of about 1012510^{125} and numerically integrating over the posterior distributions to approximate the true Bayes factor gives me about the same result which is a decisive victory for the log-linear model.

I learned a lot through this project and I really enjoyed surveying Bayesian statistics while doing background reading and was super fun all around.