Modelling branch mispredicts

26 October 2024

I was bored so I decided to benchmark some C code.

#include <stdlib.h>

#ifndef PROBABILITY
#define PROBABILITY 50
#endif

int main() {
    srand(0);
    volatile int total = 0;
    for (int i = 0; i < (1 << 27); ++i) { 
        if (rand() < RAND_MAX / 100 * PROBABILITY) {
             ++total;
        }
    }
    return 0;
}

When we compile this code we get the following disassembly output

int main() {
    1149:   55                      push   %rbp
    114a:   48 89 e5                mov    %rsp,%rbp
    114d:   48 83 ec 10             sub    $0x10,%rsp
    srand(0);
    1151:   bf 00 00 00 00          mov    $0x0,%edi
    1156:   e8 d5 fe ff ff          call   1030 <srand@plt>
    volatile int total = 0;
    115b:   c7 45 f8 00 00 00 00    movl   $0x0,-0x8(%rbp)
    for (int i = 0; i < (1 << 27); ++i) { 
    1162:   c7 45 fc 00 00 00 00    movl   $0x0,-0x4(%rbp)
    1169:   eb 19                   jmp    1184 <main+0x3b>
        if (rand() < RAND_MAX / 100 * PROBABILITY) {
    116b:   e8 d0 fe ff ff          call   1040 <rand@plt>
    1170:   3d e7 ff ff 3f          cmp    $0x3fffffe7,%eax
    1175:   7f 09                   jg     1180 <main+0x37>
             ++total;
    1177:   8b 45 f8                mov    -0x8(%rbp),%eax
    117a:   83 c0 01                add    $0x1,%eax
    117d:   89 45 f8                mov    %eax,-0x8(%rbp)
    for (int i = 0; i < (1 << 27); ++i) { 
    1180:   83 45 fc 01             addl   $0x1,-0x4(%rbp)
    1184:   81 7d fc ff ff ff 07    cmpl   $0x7ffffff,-0x4(%rbp)
    118b:   7e de                   jle    116b <main+0x22>
        }
    }
    return 0;
    118d:   b8 00 00 00 00          mov    $0x0,%eax
}
    1192:   c9                      leave
    1193:   c3                      ret

The compiler has transformed our if statement into the conditional jump instruction jg which instructs the processor to skip past the increment line if the condition is false.

Modern processors split instruction processing into different stages which are performed by different processor units, this is called pipelining and we do this so we can work on processing many different instructions at once to improve performance. For example, the classic RISC pipeline includes stages for fetching instructions, decoding instructions, executing instructions, accessing memory and writing to registers.

Pipelining generally works works well but things become tricky with conditional jumps or “branches”. When we have a branch we introduce a dependency on condition we’re branching on and this prevents us from knowing what instruction we need to put into the pipeline until the instruction that computes the condition has been evaluated.

Modern CPUs prediction employ “branch prediction” where we try and guess what will come next, if we’re correct then we effectively get to fetch the next instruction for free but if we’re wrong then we need to bin the result and start the entire process for the correct instruction, reverting all future work we’ve done based on our incorrect guess.

The Motorola M68040 processor used the simple heuristic that we usually take branches and its strategy was to predict that every branch was taken but modern CPUs use more complicated heuristics such as global and local pattern correlation which typically work by recording branching patterns in specialised hardware called the Pattern History Table.

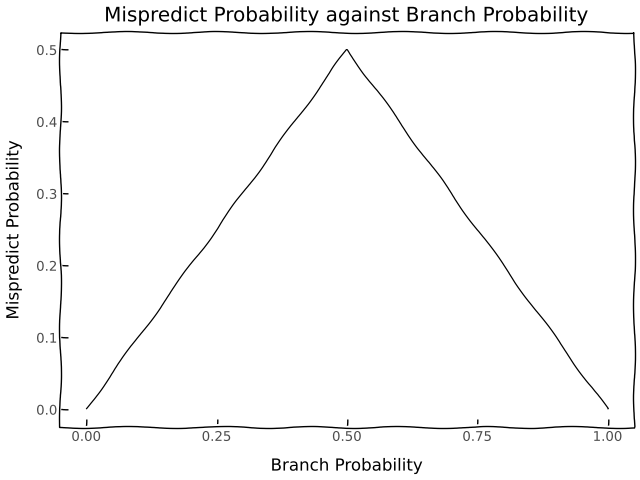
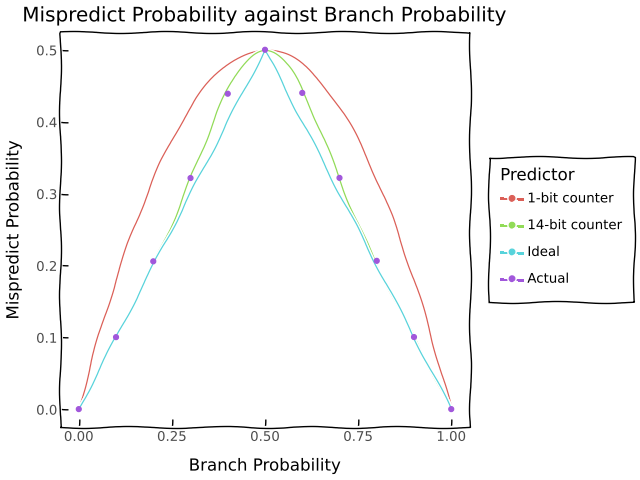
Our workload is entirely random so there aren’t any exploitable patterns we can use to predict whether or not we will take a branch. In the ideal case, we always predict the most likely outcome so if our branch probability is \(p\) we mispredict with probabiility \(\min \{p, 1 - p\} \) which looks like this on a graph.

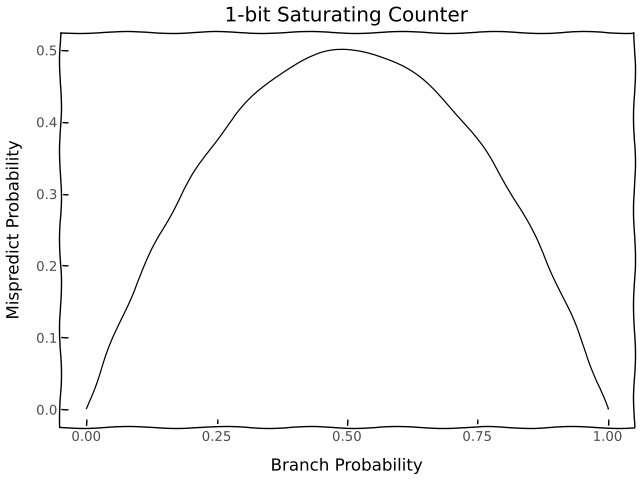
The simplest way we can approximate this is by maintaining a history of branch results and observing the most common result. If we usually take branches then we should predict that we take the next branch and if we usually don’t then we should predict that we don’t take the next branch. This is also known as a saturating counter and this idea features as part of the branch prediction system for the Intel Pentium.

If we have a 1-bit predictor where we use just 1 bit to store whether or not the previous branch was taken then the probability of a mispredict is the probability we branch now but we didn’t branch in the previous case or we don’t branch now but we branched in the previous case which is \(2p(1 - p)\)

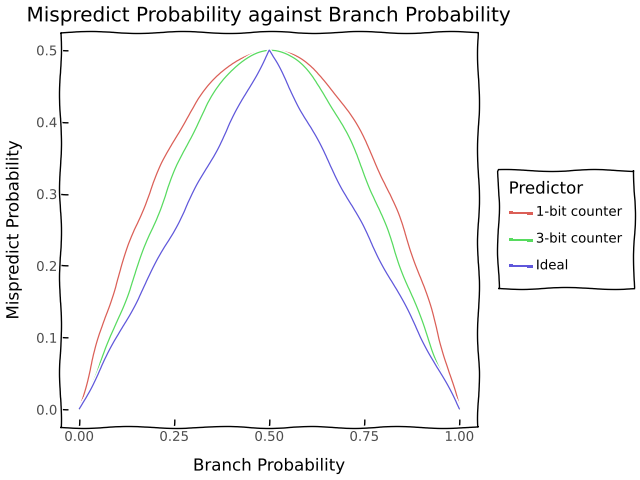
If we have a 3-bit predictor which stores the branch result from the previous 3 branch instructions then the probability of a mispredict is the probability that the most common path taken out of the previous 3 runs is not the one we take now. This is the probability that we either

• branched twice or more but not now
• branched once or less and branched now

The first case happens with probability \((1 - p)\left(3p^2\left(1 - p\right) + p^3\right)\) and the second case happens with probability \(p\left(\left(1 - p\right)^3 + 3\left(1 - p\right)^2p \right)\) so the probability of a mispredict is \( (1 - p)\left(3p^2\left(1 - p\right) + p^3\right) + p\left(\left(1 - p\right)^3 + 3\left(1 - p\right)^2p \right)\). Together these all look like these on a graph.

In general for an \(n\)-bit predictor we mispredict with probability \[ \left(p \sum_{i = 1}^{\lceil \frac{n}{2} \rceil} (1 - p)^ip^{n - i} \right) + \left( (1 - p) \sum_{i = 1}^{\lceil \frac{n}{2} \rceil} p^i(1 - p)^{n - i} \right) \]

I’m not sure if there’s a nice closed-form for this but we can use the Central Limit Theorem to approximate the number of times we branch. If \(X\) is a random variable representing the number of times we branch after \(n\) iterations then we mispredict with probability that is around \[ \begin{align*} pP\left(X < \frac{n}{2}\right) + \left(1 - p\right)P\left(X > \frac{n}{2}\right) &= pP\left(X < \frac{n}{2}\right) + \left(1 - p\right)\left(1 - P\left(X < \frac{n}{2}\right)\right) \\ &= pP\left(X < \frac{n}{2}\right) + \left(1 - p\right)\left(1 - P\left(X < \frac{n}{2}\right)\right) \\ &= \left(1 - 2p\right)P\left(X \geq \frac{n}{2}\right) + p \\ &\approx \left(1 - 2p\right)\left(1 - \Phi\left(\frac{n\left(1 - 2p\right)}{2\sqrt{np\left(1 - p\right)}}\right)\right) + p \end{align*} \]

Where \(\Phi(x)\) is the CDF for the standard normal distribution.

We can model the number of mispredicts as the sum of mispredicts from our if statement and those from other causes.

We can estimate the number of mispredicts from other causes by running the code with PROBABILITY set to either 0 or 1 and we can estimate the total number of branches from our if statement using our approximation for the mispredict probability above by running the code with PROBABILITY set to 50% and multiplying the number of mispredicts caused by our branch by 2 since, no matter what the branch prediction strategy is, we will mispredict with a probability of 50%.

After disabling compile optimisations to make sure the compiler doesn’t eliminate the branch and measuring mispredicts using perf, we get the following result.

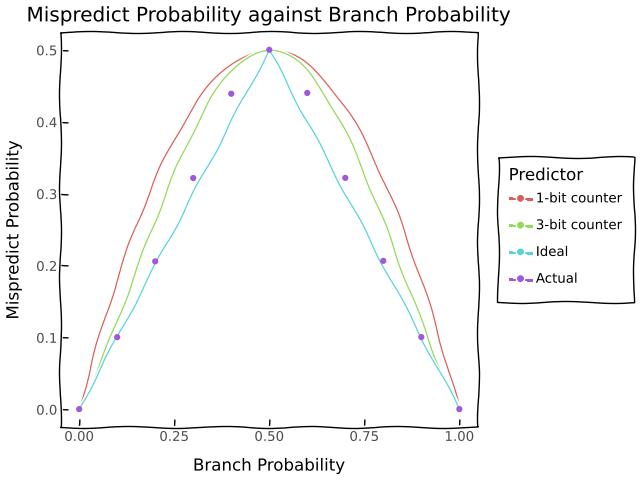
Using my approximation from earlier, we find that a \(14\)-bit counter best models the performance of my CPU on this particular workload which might motivate a cool measure of branch predictor performance on a workload in terms of \(n\)-bit counters.

This was pretty fun