Co-arrays in Fortran
28 November 2024
Fortran 2008 introduced the concept of co-arrays which, despite the name, have nothing to do with coinductive datatypes also known as codata.
In Fortran, co-arrays bring support for parallel programming to the language level with the goal of making it easier to read and write parallel code by providing a new implementation-agnostic abstraction.
You can think of co-arrays as computing the same code across identical compute units that work on separate data. These compute units are termed “images” and arrays in a program may be equipped with a co-dimension which specify how to index data based on what image they reside on.
A simple Monte Carlo simulation
For example, the following code approximates pi in parallel using a Monte Carlo simulation. In the simulation we sample points from the unit square and approximate the area of the unit circle by considering the proportion of these points occur in the first quadrant of the unit circle centred around the origin.
program main
integer :: number_of_trials = 10000000
real(8) :: x[*], y[*]
real(8) :: total[*]
integer :: trial_number
do trial_number = 1, number_of_trials
call random_number(x)
call random_number(y)
if (x**2 + y**2 < 1) then
total = total + 1
end if
end do
call co_sum(total, result_image=1)
if (this_image() == 1) then
print *, "pi is approximately", 4 * real(total) / real(number_of_trials) / num_images()
end if
end program main
The line real(8) :: x[*], y[*] declares two scalar
co-arrays x and y. The code inside the square
brackets specifies the co-dimension and in particular the *
specifies that my images are laid out in a flat grid. Had I used
x[2, *] my images would be arranged in a 2 by \(n\) grid
where \(n\) is selected so that \(2n\) is larger than or equal to the
number of images at run time.
The co_sum function sums the total array
across the co-dimension and the result_image=1 argument
specifies that the result should be stored on the first image. There are
also other reduction functions for co-arrays such as co_max
andco_min.
The RBC model of the economy
Now let’s look at writing parallel programs for economics and finance.
In the typical Real Business Cycle model we have a representative household that allocates its budget over consumption and saving to maximise a discounted inter-temporal utility function. This means that the household plans how much they consume and how much they save in each time period to maximise a consumption objective while also taking into account their budget constraint and the effects of their choices on their own future.
We formalise this as allowing the household to plan consumption amounts \(c_t\) for every time period. We assume that the utility gained from consumption is modelled by the isoelastic utility function which takes the form \(u(c_t) = \frac{c_t^{1 - \eta}}{1 - \eta} \). Where \(\eta\) is a parameter corresponding to risk aversion.
The household then seeks to maximise time-discounted utility, which we can interpret as valuing consumption today more than they value consumption in the future. This time-discounted utility looks like this
\[\mathbb E_0 \sum_{t = 0}^\infty \beta^t u(c_t) \]
Where \(\beta\) is termed the “discount factor”. When \(\beta\) is less than one, the \(\beta^t\) factor decreases for each time period in the future which has the effect of exponentially reducing the relative weight of consumption in the future. Here \(\mathbb E_0\) refers to the household’s expectation at the current time period \(t = 0\).
The household is subject to the following budget constraint
\[c_t + i_t = w_t + r_tk_t\]
Where \(i_t\) refers to the amount saved at time \(t\), \(w_t\) refers to the wage or income at time \(t\), \(r_t\) refers to the saving rate and \(k_t\) refers to wealth at time \(t\). This constraint states that we can only spend and save as much money as we have which is the total amount gained from income and from existing savings.
Wealth is accumulated according to following rule
\[k_{t+1} = (1 - \delta) k_t + i_t\]
Where \(\delta\) is a depreciation factor for wealth. This indicates that our wealth in the next time step is equal to the sum our wealth in the current time step accouted for depreciation and how much we save in the current time step.
In the RBC model there’s a representative firm that produces output \(y_t = z_tk_t^\alpha\) that is a function of productivity, \(z_t\) and capital, \(k_t\).
Productivity is modelled as changing according to an AR(1) process.
\[\log z_t = \rho \log z_{t-1} + \epsilon_t\]
Where \(\epsilon_t \sim \mathcal N(0, \sigma^2) \) epsilon is stochastic white noise to add uncertainty to the simulation.
We can solve this system by interpreting the household’s planning problem using a value function \(V\) and a Bellman operator which we can solve using value function iteration. The household’s value function computes to the following form
\[ V(k, z) = \max_c \left \{ \frac{c^{1 - \eta}}{1 - \eta} + \beta \mathbb E\left[V(k’, z’)|z\right] \right \} \]
And this is subject to the following constraint
\[k’ = zk^\alpha + (1 - \delta)k - c\]
Value function iteration works by first observing that a suitable value function must satisfy \(V(x) = u(x) + \max_x \beta V(x’)\) which is recursive in \(V\). As such we can update \(V\) using this equation until we converge on a function.
Fortran 2008 also introduced the do concurrent syntax
which specifies that we may perform iterations of a loop in parallel.
For simple applications like Value Function Iteration I can use
do concurrent without needing to use co-arrays.
In my code, I first quantise my grid into a finite number of points and then I perform value function iteration. I ignore the stochastic factor for ease of implementation.
program main
implicit none
real(8), parameter :: MAX_WEALTH = 100
real(8), parameter :: MAX_PRODUCTIVITY = 2
real(8), parameter :: MAX_CONSUMPTION = 100
integer, parameter :: NUMBER_OF_POINTS = 100
real(8), dimension(NUMBER_OF_POINTS, NUMBER_OF_POINTS, NUMBER_OF_POINTS) :: V
real(8), dimension(NUMBER_OF_POINTS, NUMBER_OF_POINTS, NUMBER_OF_POINTS) :: V_prime
integer :: consumption_index, wealth_index, productivity_index
real(8) :: consumption, wealth
real(8), parameter :: beta = 0.984
real(8), parameter :: eta = 2
real(8), parameter :: alpha = 0.35
real(8), parameter :: delta = 0.01
real(8), parameter :: rho = 0.95
real(8), parameter :: sigma = 0.005
integer, parameter :: MAX_ITERATIONS = 200
integer :: iteration
! Simulation variables
integer, parameter :: number_of_timesteps = 10
real(8) :: wage = 1
real(8) :: interest_rate = 1.05
real(8), dimension(number_of_timesteps) :: model_time, model_consumption, model_productivity, model_wealth
real(8) :: epsilon
call random_number(V)
V_prime = 0
do iteration = 1, MAX_ITERATIONS
do concurrent ( &
consumption_index = 1:NUMBER_OF_POINTS, &
wealth_index = 1:NUMBER_OF_POINTS, &
productivity_index = 1:NUMBER_OF_POINTS &
)
if (consumption_index > wealth_index) then
continue
end if
V_PRIME(consumption_index, wealth_index, productivity_index) = &
utility(dequantise(consumption_index, MAX_CONSUMPTION)) &
+ beta * maxval(V(:, &
quantise( &
dequantise(productivity_index, MAX_PRODUCTIVITY)**rho &
* dequantise(wealth_index, MAX_WEALTH) ** alpha &
+ quantise((1 - delta) * dequantise(wealth_index, MAX_WEALTH), MAX_WEALTH) &
- dequantise(consumption_index, MAX_CONSUMPTION), &
MAX_WEALTH &
), &
quantise(dequantise(productivity_index, MAX_PRODUCTIVITY) ** rho, MAX_PRODUCTIVITY)))
end do
sync all
if (this_image() == 1) then
print *, "iteration", iteration
V = V_PRIME
end if
end do
if (this_image() == 1) then
model_consumption(1) = 1
model_wealth(1) = 10
model_productivity(1) = 1
do iteration = 2, number_of_timesteps
call random_number(epsilon)
model_time(iteration) = iteration
model_productivity(iteration) = model_productivity(iteration - 1)**rho * exp(epsilon * 2 - 1)
model_consumption(iteration) = dequantise( &
maxloc( &
V(:, &
quantise(model_wealth(iteration - 1), MAX_WEALTH), &
quantise(model_productivity(iteration), MAX_PRODUCTIVITY) &
), &
1 &
), &
MAX_CONSUMPTION &
)
model_wealth(iteration) = &
model_productivity(iteration - 1) * model_wealth(iteration - 1)**alpha &
+ (1 - delta) * model_wealth(iteration - 1) &
- model_consumption(iteration - 1) + wage
end do
do iteration = 1, number_of_timesteps
print *, model_consumption(iteration)
end do
end if
contains
pure function dequantise(quantity_index, max_value)
integer, intent(in) :: quantity_index
real(8), intent(in) :: max_value
real(8) :: dequantise
dequantise = (quantity_index - 1) / real(NUMBER_OF_POINTS) * real(max_value)
end function
pure function clamp(x, minimum, maximum)
real(8), intent(in) :: x, minimum, maximum
real(8) :: clamp
clamp = min(max(x, minimum), maximum)
end function
pure function quantise(quantity, max_value)
real(8), intent(in) :: quantity, max_value
integer :: quantise
quantise = max( &
int(clamp(quantity, real(0, 8), max_value) / max_value * NUMBER_OF_POINTS) + 1, &
NUMBER_OF_POINTS)
end function
pure function utility(consumption)
real(8), intent(in) :: consumption
real(8) :: utility
utility = consumption ** (1 - eta) / (1 - eta)
end function
end program mainI simplified the model in a few places. For example, productivity growth is entirely deterministic and I completely removed the stochastic factor.
The VFI converges and the simulation converges to a steady state of consumption which is good and expected however the simulation converges unusually fast so I’ll take a closer look to figure out what’s going on.
Pricing options
Now, I want to write some code for pricing options.
In Finance, a derivative is a financial instrument whose value is derived from another asset such as a stock. For example, a forward is a financial contract that arranges the future sale of an asset at an agreed price. An example forward contract would permit me to purchase one share of Google (GOOG) one year from now at the price of $172. How much should such a contract cost?
In Finance, there’s the concept of the time value of money. It formalises the notion of “money today is worth more than money tommorow”. Would you rather I give you $1,000 today or $1,000 three years from now? One intuitive reason for why this is true is that, due to inflation, $1,000 today can buy more than $1,000 three years from now.
For example, I could by 10 Freddo bars for £1 in 2000 however now I can only by a measly three Freddo bars.
Another intuitive reason is the interest rate and this ties in with the demand for money. One interpretation of the interest rate is as the answer to the question of “how much would you pay for access to money now?”. We can see this with the Federal Funds Effective Rate or another overnight lending rate such as SONIA.
If a bank has an obligation that requires them to hold more money, then they will need to purchase it for a price and this price is called the interest rate.
An interesting consequence of this interpretation is that we can use the interest rate as a metric for stress or pressure in the financial market. In unsecured lending markets, the interest rate tends to be higher as the lender would like to ask for a “premium” to compensate for the risk involved. The difference between this rate and a more secure rate is called a spread and a high spread indicates strain or uncertainty in the market.
Interlude
As a quick digression before going back to the time value of money, SONIA is a new interest rate average that replaced Libor. Libor was effectively a survey from banks about the rates they would lend at. However, it was discontinued due to fraud as respondents lied abot the rates they would offer.
Interest rates, Futures and the Time Value of Money
Lets say that we have an interest rate \(r\) that is continually compounded. So I can lend a dollar for a time period, \(t\) and at maturity I will be owed \(e^{rt}\) dollars. Putting this in reverse, I can effectively buy a dollar from the future for \(e^{-rt}\) dollars today. We’re going to use this fact while pricing options.
A naive attempt of pricing a future would be by considering the expected value of the option at the time of maturity. For example, I could construct such a contract by waiting for a year then purchasing the stock at the time at maturity for the agreed upon price, this price is called the forward price.
Let the forward price be \(F\), the time of maturity be \(T\) and the stock price at the time of maturity be \(S_T\). If I use this construction, I will make a profit of \(F - S_T\) at the time of maturity. Adjusting for the time difference and the time value of money, this becomes \(e^{-rT}(F - S_T)\) so this suggest that the value of this contract is thus \(\mathbb E \left[ e^{-rT}(F - S_T) \right] \) and we break even when this is equal to 0 which occurs when \(F = \mathbb E \left[S_T\right]\) and the forward price is the expected price of the stock at time \(T\).
If we assume that the log-return from holding this stock, \(X \sim N(\mu, \sigma^2)\), is normally distributed with mean \(\mu\) and standard deviation \(\sigma\) then we get the following equation describing the stock price.
\[ \begin{align*} \log S_T &= \log S_0 + X \\ S_T &= S_0 e^X \\ \end{align*} \]
After integrating we get \(\mathbb E \left[ S_T \right] = S_0e^{\mu + \frac{\sigma^2}{2}}\).
However, to quote this price would be incorrect as there is an arbitrage opportunity and in reality I can construct this contract cheaper.
To construct this contract, I could alternatively borrow the money to purchase this stock right now which will cost me \(S_0e^{rT}\) and simply hold onto it until the forward contract matures and this construction upper-bounds the fair price of this future.
Options
In Finance, a European-style option is a contract that grants the purchaser the right to buy a stock at a specific price, the “strike price” on a certain date. So it is like a Forward contract in that we may buy the stock at the agreed price at the time of maturity but it differs in that we have the option to not do this.
If the value of the stock is higher than the contract’s strike price, \(K\), then we can buy the stock at the strike price and sell the stock at the market price, yielding us a profit of \(K - S_T\). If the strike price is higher than the stock price then the contract is worthless and our profit is 0 since it’s cheaper to buy the stock at the market price and it doesn’t make sense to exercise our option.
Using this strategy, the value of our contract at time \(T\) is \(\max \{K - S_T, 0\}\) so the expected value of our contract now is \(e^{-rt}\mathbb E \left[ \max \{K - S_T, 0\}\right]\).
How do we calculate the expectation of the stock price? If we have a stochastic model for how the price of our stock evolves over time then we can evaluate it numerically by using another Monte Carlo simulation.
Recall from earlier that log returns over a fixed time period are typically normally distributed. So we can set up a stochastic differential equation modelling the motion of the log of stock price. If we let \(r_t = \log S_t\) and assume continuity and independent increments then if \(W_t\) is a Weiner process then we have
\[ dr_t = \mu dt + \sigma dW_t \]
After integrating this we get \[ \begin{align*} \int_0^T dr_tdt &= \int_0^T\mu dt + \int_0^T \sigma dW_t \\ r_T &= \mu T + \sigma \int_0^T dW_t \end{align*} \]
Which is an Itô process that we can use Itô’s lemma with \(f(x, t) = e^x\) to describe the motion of the stock price as an Itô process. After doing this, we get
\[ \begin{align*} dS_t &= \left( \mu e^{r_t} + \frac{\sigma^2}{2} e^{r_t} \right) dt + \sigma e^{r_t}dW_t \\ dS_t &= (\mu S_t + \frac{\sigma^2}{2}S_t)dt + S_tdW_t \\ dS_t &= S_t \left( \mu + \frac{\sigma^2}{2} \right)dt + \sigma S_TdW_t \end{align*} \]
This describes Geometric Brownian Motion which we typically use to model stock prices.
When I wrote my code to price options, I used a Jump diffusion model which is very similar except we model the stock price as being affected by discontinuous jumps. We model the number of jumps occuring in a fixed period, \(N_t\), as a poisson distributed random variable,and we model the magnitude of these jumps, \(Q_i\) as a normally distributed random variable with constant mean and standard deviation.
Our difference equation now looks like
\[ dr_T = \mu dt + \sigma dW_t + \sum_{i=1}^{N_t}Q_i \]
If we make the assumption that we see at most 1 jump in a time period or equivalently \(N_t\) is either 0 or 1 we can simplify this to
\[ dr_T = \mu dt + \sigma dW_t + N_tQ_t \]
Which is the sum of brownian motion and another stochastic process that’s the combination of normally distributed random variables and poisson distributd random variables.
I again used Fortran co-arrays to write parallelised code to simulate potential paths of the stock using the 6 cores of my laptop.
I sampled from the normal distribution using the Box-Muller transform and I sample from the poisson distribution using a technique from Knuth’s The Art of Computer Programming.
I list some example price paths from my simulation below. In the second image I increase the expected jump size to better illustrate the jump diffusion model.
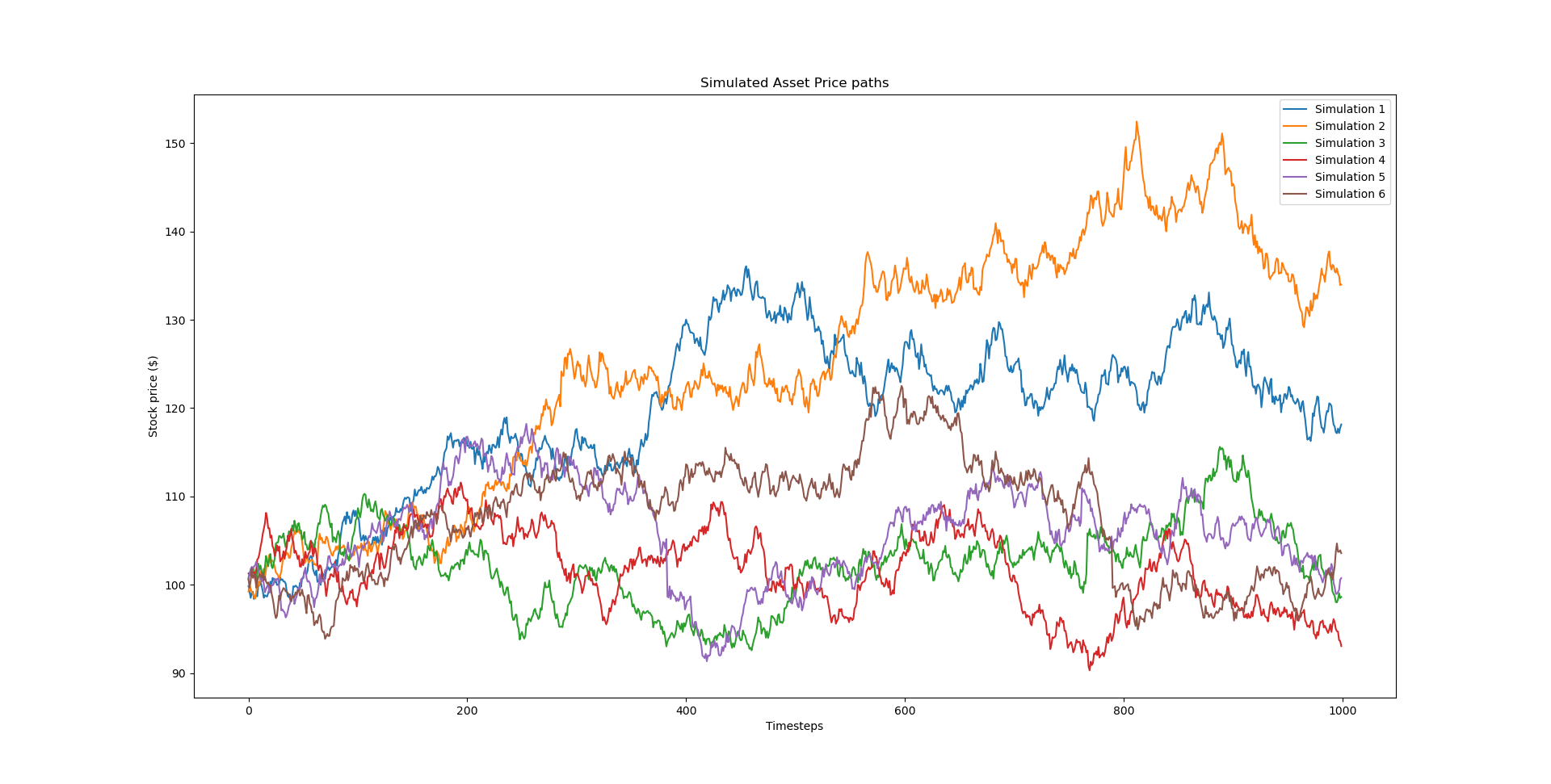
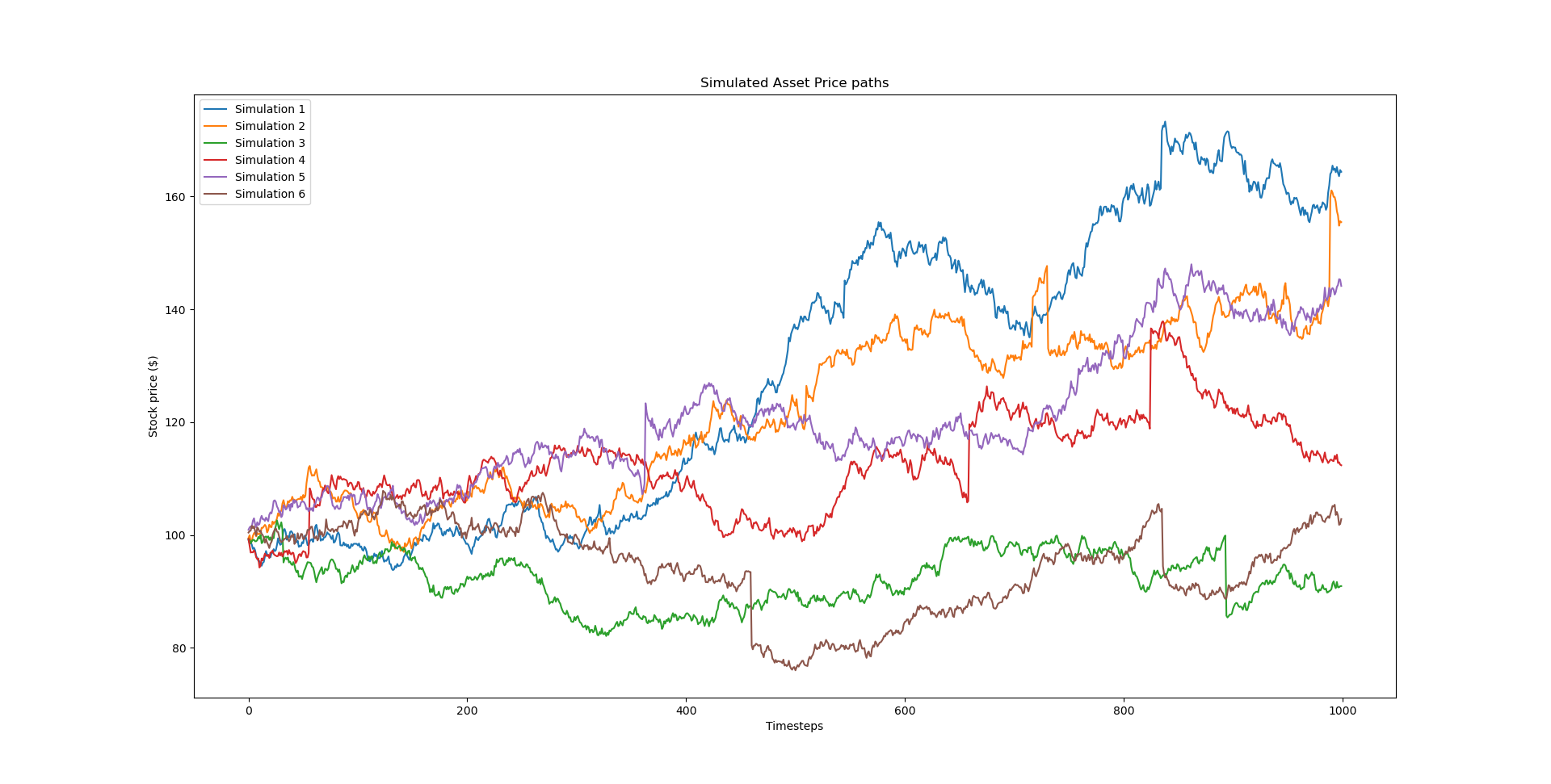
My code looks like this
program main
implicit none
! Initial stock price
real(8), parameter :: S0 = 100
! Strike price
real(8), parameter :: K = 110
! Time to maturity in years
real(8), parameter :: T = 1
! Risk free rate
real(8), parameter :: r = 0.02
! Volatility
real(8), parameter :: volatility = 0.2
! Number of jumps per year
real(8), parameter :: expected_number_of_jumps = 2
! Mean jump size
real(8), parameter :: mean_jump_size = 0
! Jump size standard deviation
real(8), parameter :: jump_volatility = 0.3
integer, parameter :: number_of_simulations = 1
integer, parameter :: number_of_timesteps = 1000
real(8), parameter :: dt = T / number_of_timesteps
real(8), dimension(number_of_timesteps, number_of_simulations) :: S[*]
real(8), dimension(number_of_timesteps, number_of_simulations) :: W1[*], W2[*]
real(8), dimension(number_of_timesteps, number_of_simulations) :: poisson, brownian_motion
integer :: simulation, iteration
integer :: image
do simulation = 1, number_of_simulations
do iteration = 1, number_of_timesteps
poisson(iteration, simulation) = rpoisson(expected_number_of_jumps * dt) * rnorm(mean_jump_size, jump_volatility)
brownian_motion(iteration, simulation) = &
( &
r &
- (volatility**2 - expected_number_of_jumps * (mean_jump_size + jump_volatility ** 2)) / 2 &
) * dt &
+ volatility * sqrt(dt) * rnorm(0.d0, 1.d0)
end do
end do
do iteration = 2, number_of_timesteps
poisson(iteration, :) = poisson(iteration - 1, :) + poisson(iteration, :)
brownian_motion(iteration, :) = brownian_motion(iteration - 1, :) + brownian_motion(iteration, :)
end do
S = S0 * exp(brownian_motion + poisson)
sync all
if (this_image() .eq. 1) then
do image = 1, num_images()
print *, S(:, 1)[image]
end do
end if
contains
function runiform()
real(8) :: runiform
call random_number(runiform)
end function
function rnorm(mu, sigma)
! Box-muller transform
real(8) :: rnorm
real(8) :: u1, u2
real(8) :: pi = 4.d0 * atan(1.d0)
real(8) :: mu, sigma
call random_number(u1)
call random_number(u2)
rnorm = mu + sigma * sqrt(-2 * log(u1)) * cos(2 * pi * u2)
end function
function rpoisson(lambda)
real(8) :: rpoisson
real(8), intent(in) :: lambda
real(8) :: threshold, uniform_product
threshold = exp(-lambda)
rpoisson = -1
uniform_product = 1
do while (threshold < uniform_product)
uniform_product = uniform_product * runiform()
rpoisson = rpoisson + 1
end do
end function rpoisson
end program mainPricing options now just becomes a case of taking an average of \(\max\{S_T, 0\}\) over all the generated paths.
This was a pretty fun project.
References
[1]: Fernández-Villaverde, Jesús, and David Zarruk Valencia. A practical guide to parallelization in economics. No. w24561. National Bureau of Economic Research, 2018.
[2]: Aldrich, Eric M., et al. “Tapping the supercomputer under your desk: Solving dynamic equilibrium models with graphics processors.” Journal of Economic Dynamics and Control 35.3 (2011): 386-393.
[3]: Peng, Ying, et al. “Parallel computing for option pricing based on the backward stochastic differential equation.” High Performance Computing and Applications: Second International Conference, HPCA 2009, Shanghai, China, August 10-12, 2009, Revised Selected Papers. Springer Berlin Heidelberg, 2010.
[4]: Baxter, Martin, and Andrew Rennie. Financial calculus: an introduction to derivative pricing. Cambridge university press, 1996.
[5]: Merton, Robert C. “Option pricing when underlying stock returns are discontinuous.” Journal of financial economics 3.1-2 (1976): 125-144.
[6]: Knuth, Donald E. The Art of Computer Programming: Seminumerical Algorithms, Volume 2. Addison-Wesley Professional, 2014.